摘要：由此猜想:．------------------------2分用数学归纳法证明如下:
网址：http://m.1010jiajiao.com/timu_id_491673[举报]
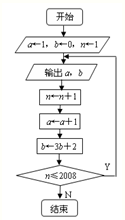根据如图所示的程序框图，将输出a，b的值依次分别记为a1，a2，…，an，…，a2008；b1，b2，…，bn，…，b2008．（Ⅰ）求数列 { an} 的通项公式；
（Ⅱ）写出b1，b2，b3，b4，由此猜想{ bn}的通项公式，并证明你的证明；
（Ⅲ）在 ak与 ak+1中插入bk+1个3得到一个新数列 { cn }，设数列 { cn }的前n项和为Sn，问是否存在这样的正整数m，使数列{ cn }的前m项的和Sm=2008，如果存在，求出m的值，如果不存在，请说明理由．
． 查看习题详情和答案>>
已知f(x)=
(x≠-a)，且f（2）=1．
（Ⅰ）求a的值；
（Ⅱ）若在数列{an}中，a1=1，an+1=f(an)，(n∈N*)，计算a2，a3，a4，并由此猜想通项公式an；
（Ⅲ）证明（Ⅱ）中的猜想．
查看习题详情和答案>>
| ax | a+x |
（Ⅰ）求a的值；
（Ⅱ）若在数列{an}中，a1=1，an+1=f(an)，(n∈N*)，计算a2，a3，a4，并由此猜想通项公式an；
（Ⅲ）证明（Ⅱ）中的猜想．
设数列{an}满足a1=2，an+1=
-nan+1，n∈N*．
（Ⅰ）求a2，a3，a4，并由此猜想an的一个通项公式，证明你的结论；
（Ⅱ）若bn=an-1，不等式
+
+…+
＞
对一切n∈N*都成立，求正整数m的最大值．
查看习题详情和答案>>
| a | 2 n |
（Ⅰ）求a2，a3，a4，并由此猜想an的一个通项公式，证明你的结论；
（Ⅱ）若bn=an-1，不等式
| 1 |
| n+b1 |
| 1 |
| n+b2 |
| 1 |
| n+bn |
| m |
| 24 |