摘要:⑵“3 原则的应用:若随机变量ξ服从正态分布则 ξ落在内的概率为99.7% 亦即落在之外的概率为0.3%.此为小概率事件.如果此事件发生了.就说明此种产品不合格. 高中数学第十三章-极 限考试内容: 教学归纳法.数学归纳法应用. 数列的极限. 函数的极限.根限的四则运算.函数的连续性.考试要求:(1)理解数学归纳法的原理.能用数学归纳法证明一些简单的数学命题.(2)了解数列极限和函数极限的概念.(3)掌握极限的四则运算法则,会求某些数列与函数的极限.(4)了解函数连续的意义.了解闭区间上连续函数有最大值和最小值的性质.
网址:http://m.1010jiajiao.com/timu_id_491067[举报]
以Φ(x)表示标准正态总体在区间(-∞,x)内取值的概率,若随机变量ξ服从正态分布N(μ,σ2),则概率P(|ξ-μ|<σ)等于( )
| A、Φ(μ+σ)-Φ(μ-σ) | ||
| B、Φ(1)-Φ(-1) | ||
C、Φ(
| ||
| D、2Φ(μ+σ) |
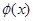 表示标准正态总体在区间(
表示标准正态总体在区间(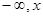 )内取值的概率,若随机变量
)内取值的概率,若随机变量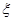 服从正态分布
服从正态分布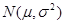 ,则概率
,则概率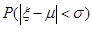 等于
等于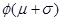 -
-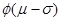 (B)
(B)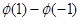
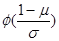 (D)
(D)