摘要：②根据组合定义与加法原理得,在确定n+1个不同元素中取m个元素方法时.对于某一元素.只存在取与不取两种可能.如果取这一元素.则需从剩下的n个元素中再取m-1个元素.所以有C.如果不取这一元素.则需从剩余n个元素中取出m个元素.所以共有C种.依分类原理有. ⑷排列与组合的联系与区别.联系:都是从n个不同元素中取出m个元素.区别:前者是“排成一排 .后者是“并成一组 .前者有顺序关系.后者无顺序关系.⑸①几个常用组合数公式
网址：http://m.1010jiajiao.com/timu_id_490939[举报]
下面结论错误 的序号是
①比较2n与2（n+1），n∈N*的大小时，根据n=1，2，3时，2＜4，4＜6，8=8，可得2n≤2（n+1）对一切n∈N*成立；
②由“（a•b）c=a（b•c）”（a，b，c∈R）类比可得“(
•
)•
=
•(
•
)”；
③复数z满足z•
=1，则|z-2+i|的最小值为
．
查看习题详情和答案>>
①②③
①②③
．①比较2n与2（n+1），n∈N*的大小时，根据n=1，2，3时，2＜4，4＜6，8=8，可得2n≤2（n+1）对一切n∈N*成立；
②由“（a•b）c=a（b•c）”（a，b，c∈R）类比可得“(
| a |
| b |
| c |
| a |
| b |
| c |
③复数z满足z•
. |
| z |
| 5 |
下面结论错误 的序号是______．
①比较2n与2（n+1），n∈N*的大小时，根据n=1，2，3时，2＜4，4＜6，8=8，可得2n≤2（n+1）对一切n∈N*成立；
②由“（a•b）c=a（b•c）”（a，b，c∈R）类比可得“(
•
)•
=
•(
•
)”；
③复数z满足z•
=1，则|z-2+i|的最小值为
．
查看习题详情和答案>>
①比较2n与2（n+1），n∈N*的大小时，根据n=1，2，3时，2＜4，4＜6，8=8，可得2n≤2（n+1）对一切n∈N*成立；
②由“（a•b）c=a（b•c）”（a，b，c∈R）类比可得“(
| a |
| b |
| c |
| a |
| b |
| c |
③复数z满足z•
| . |
| z |
| 5 |
下面结论错误 的序号是 ．
①比较2n与2（n+1），n∈N*的大小时，根据n=1，2，3时，2＜4，4＜6，8=8，可得2n≤2（n+1）对一切n∈N*成立；
②由“c=a”（a，b，c∈R）类比可得“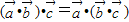
”；
③复数z满足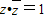
，则|z-2+i|的最小值为
．
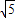查看习题详情和答案>>
①比较2n与2（n+1），n∈N*的大小时，根据n=1，2，3时，2＜4，4＜6，8=8，可得2n≤2（n+1）对一切n∈N*成立；
②由“c=a”（a，b，c∈R）类比可得“
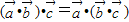”；③复数z满足
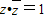，则|z-2+i|的最小值为．
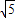查看习题详情和答案>>
下面结论错误 的序号是________．
①比较2n与2（n+1），n∈N*的大小时，根据n=1，2，3时，2＜4，4＜6，8=8，可得2n≤2（n+1）对一切n∈N*成立；
②由“（a•b）c=a（b•c）”（a，b，c∈R）类比可得“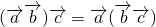
”；
③复数z满足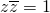
，则|z-2+i|的最小值为
．
查看习题详情和答案>>
若某产品的直径长与标准值的差的绝对值不超过1mm 时，则视为合格品，否则视为不合格品。在近期一次产品抽样检查中，从某厂生产的此种产品中，随机抽取5000件进行检测，结果发现有50件不合格品。计算这50件不合格品的直径长与标准值的差（单位：mm）, 将所得数据分组，得到如下频率分布表：
|
分组 |
频数 |
频率 |
|
[-3, -2) |
|
0.10 |
|
[-2, -1) |
8 |
|
|
（1,2] |
|
0.50 |
|
（2,3] |
10 |
|
|
（3,4] |
|
|
|
合计 |
50 |
1．00 |
（Ⅰ）将上面表格中缺少的数据填在答题卡的相应位置；
（Ⅱ）估计该厂生产的此种产品中，不合格品的直径长与标准值的差落在区间（1,3]内的概率；
（Ⅲ）现对该厂这种产品的某个批次进行检查，结果发现有20件不合格品。据此估算这批产品中的合格品的件数。
【解析】（Ⅰ）
|
分组 |
频数 |
频率 |
|
[-3, -2) |
5 |
0.10 |
|
[-2, -1) |
8 |
0.16 |
|
（1,2] |
25 |
0.50 |
|
（2,3] |
10 |
0.2 |
|
（3,4] |
2 |
0.04 |
|
合计 |
50 |
1．00 |
（Ⅱ）根据频率分布表可知，落在区间（1,3]内频数为35，故所求概率为0.7.
（Ⅲ）由题可知不合格的概率为
0.01，故可求得这批产品总共有2000，故合格的产品有1980件。
查看习题详情和答案>>