题目内容
下面结论错误 的序号是
①比较2n与2（n+1），n∈N*的大小时，根据n=1，2，3时，2＜4，4＜6，8=8，可得2n≤2（n+1）对一切n∈N*成立；
②由“（a•b）c=a（b•c）”（a，b，c∈R）类比可得“(
•
)•
=
•(
•
)”；
③复数z满足z•
=1，则|z-2+i|的最小值为
．
①②③
①②③
．①比较2n与2（n+1），n∈N*的大小时，根据n=1，2，3时，2＜4，4＜6，8=8，可得2n≤2（n+1）对一切n∈N*成立；
②由“（a•b）c=a（b•c）”（a，b，c∈R）类比可得“(
| a |
| b |
| c |
| a |
| b |
| c |
③复数z满足z•
. |
| z |
| 5 |
分析：对于①利用数学归纳法，判断正误即可；
对于②通过类比推理，可以判断向量关系的正误；
通过复数的几何意义，直接求出模的大小，判断正误即可．
对于②通过类比推理，可以判断向量关系的正误；
通过复数的几何意义，直接求出模的大小，判断正误即可．
解答：解：①比较2n与2（n+1），n∈N*的大小时，根据n=1，2，3时，2＜4，4＜6，8=8，可得2n≤2（n+1）对一切n∈N*成立；这显然是不正确的，没有满足数学归纳法的证明步骤，当n=4时16＜10，不正确；
②由“（a•b）c=a（b•c）”（a，b，c∈R）类比可得“(
•
)•
=
•(
•
)”；这是不正确的，(
•
)•
表示向量
方向上的向量，
•(
•
)表示
向量方向的向量，二者不相等，不正确；
③复数z满足z•
=1，表示单位圆，则|z-2+i|表示单位圆上的点到（-2，1）的距离，它的最小值为
-1．③不正确；
故答案为：①②③．
②由“（a•b）c=a（b•c）”（a，b，c∈R）类比可得“(
| a |
| b |
| c |
| a |
| b |
| c |
| a |
| b |
| c |
| c |
| a |
| b |
| c |
| a |
③复数z满足z•
. |
| z |
| 5 |
故答案为：①②③．
点评：本题是中档题，考查数学归纳法的应用，类比推理和复数的模的应用，考查计算能力，逻辑推理能力．
练习册系列答案
相关题目
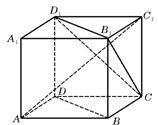6、如图，ABCD-A1B1C1D1为正方体，下面结论错误的序号是
”；
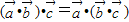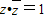，则|z-2+i|的最小值为
．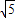