摘要:17.一商家诚邀甲.乙两名围棋高手进行一场网络围棋比赛.每比赛一局商家要向每名棋手支付200元对局费,同时从转让网络转播权及广告宣传中获利1000元.从两名棋手以往的比赛中得知: 甲每局获胜的概率为,乙每局获胜的概率为,若两名棋手约定:最多下五局,最先连胜两局者获胜,比赛结束.(1)下完五局且甲获胜的概率是多少?(2)商家从这场网络棋赛中获得的收益的数学期望是多少?解: (1)设下完五局且甲获胜为事件A,则5局的胜负依次为: 乙胜.甲胜.乙胜.甲胜.甲胜.
网址:http://m.1010jiajiao.com/timu_id_49088[举报]
一、选择题:本大题共10小题,每小题5分,共50分。在每小题给出的四个选项中,只有 一项是符合题目要求的。
题号
1
2
3
4
5
6
7
8
9
10
答案
二、填空题:(本大题共5个小题,每小题5分,共25分,)
11. 12. 13. 14. 15.
三、解答题:
(本题满分12分)
一汽车厂生产A、B、C三类轿车,每类轿车有豪华型和标准型两种型号,某月生产情况如下表(单位:辆)
|
|
轿车A |
轿车B |
轿车C |
|
舒适型 |
100 |
150 |
x |
|
标准型 |
300 |
450 |
600 |
按分层抽样的方法在这个月生产的轿车中抽取50辆,其中有A类轿车10辆.
(I)求x的值;
(I)列出所有基本事件,并求出至少有一辆是豪华型轿车的概率.
查看习题详情和答案>>
(本题满分12分)一盒子中有8个大小完全相同的小球,其中3个红球,2个白球,3个黑球.
(Ⅰ)若不放回地从盒中连续取两次球,每次取一个,求在第一次取到红球的条件下,第二次也取到红球的概率;
(Ⅱ)若从盒中任取3个球,求取出的3个球中红球个数X的分布列和数学期望.
查看习题详情和答案>>
(本题满分12分)
一辆货车的最大载重量为 吨,要装载
吨,要装载 、
、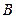 两种不同的货物,已知装载
两种不同的货物,已知装载 货物每吨收入
货物每吨收入 元,装载
元,装载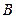 货物每吨收入
货物每吨收入 元,且要求装载的
元,且要求装载的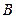 货物不少于
货物不少于 货物的一半.请问
货物的一半.请问 、
、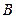 两种不同的货物分别装载多少吨时,载货得到的收入最大?并求出这个最大值.
两种不同的货物分别装载多少吨时,载货得到的收入最大?并求出这个最大值.
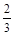 .,每次命中与否互相独立.
.,每次命中与否互相独立.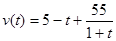 (单位:m/s)紧急刹车至停止。求:
(单位:m/s)紧急刹车至停止。求: