题目内容
（本题满分12分）一盒子中有8个大小完全相同的小球，其中3个红球，2个白球，3个黑球.
（Ⅰ）若不放回地从盒中连续取两次球，每次取一个，求在第一次取到红球的条件下，第二次也取到红球的概率；
（Ⅱ）若从盒中任取3个球，求取出的3个球中红球个数X的分布列和数学期望.
【答案】
（Ⅰ）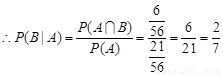
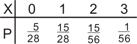
（Ⅱ）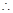 
X的分布列为
X的数学期望为：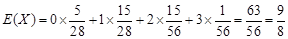 
【解析】解:（Ⅰ）设事件A=“第一次取到红球”，事件B=“第二次取到红球”
由于是不放回地从盒中连续取两次球，每次取一个，所以第一次取球有8种方法，第二次取球是7种方法，一共的基本事件数是56，
由于第一次取到红球有3种方法，第二次取球是7种方法，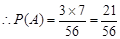
… 2分
又第一次取到红球有3种方法，由于采取不放回取球，所以第二次取到红球有2种方法，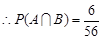
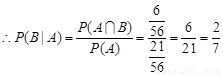……4分
（Ⅱ）从盒中任取3个球，取出的3个球中红球个数X的可能值为0,1,2,3…… 5分
且有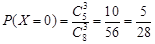 
, 
,
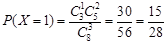
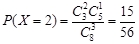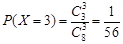…… 9分
X的分布列为 …… 10分
X的数学期望为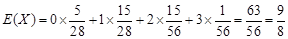： ……12分
练习册系列答案
开心蛙口算题卡系列答案
相关题目
吨，要装载
、
两种不同的货物，已知装载
元，装载
的数学期望
。
的左、右顶点分别为
，点
是双曲线上不同的两个动点。
与
交点的轨迹
的方程式；
与曲线
，已知点
的坐标为
，若点
在线段
的垂直平分线上，且
.求
的值.（本题满分12分）
一汽车厂生产A、B、C三类轿车，每类轿车有豪华型和标准型两种型号，某月生产情况如下表（单位：辆）
|
|
轿车A |
轿车B |
轿车C |
|
舒适型 |
100 |
150 |
x |
|
标准型 |
300 |
450 |
600 |
按分层抽样的方法在这个月生产的轿车中抽取50辆,其中有A类轿车10辆.
（I）求x的值；
（I）列出所有基本事件，并求出至少有一辆是豪华型轿车的概率.
