⑴最小角定理:(为最小角.如图)⑵最小角定理的应用简记为:成角比交线夹角一半大.且又比交线夹角补角一半长.一定有4条.成角比交线夹角一半大.又比交线夹角补角小.一定有2条.成角比交线夹角一半大.又与——青夏教育精英家教网——

摘要： ⑴最小角定理:(为最小角.如图)⑵最小角定理的应用简记为:成角比交线夹角一半大.且又比交线夹角补角一半长.一定有4条.成角比交线夹角一半大.又比交线夹角补角小.一定有2条.成角比交线夹角一半大.又与交线夹角相等.一定有3条或者2条.成角比交线夹角一半小.又与交线夹角一半小.一定有1条或者没有. 五. 棱锥.棱柱.

网址：http://m.1010jiajiao.com/timu_id_490836[举报]

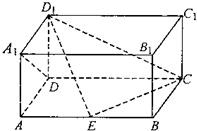如图，在长方体ABCD-A₁B₁C₁D₁中，AD=AA₁=1，AB＞1，点E在棱AB上移动，小蚂蚁从点A沿长方体的表面爬到点C₁，所爬的最短路程为2

．
（1）求证：D₁E⊥A₁D；
（2）求AB的长度；
（3）在线段AB上是否存在点E，使得二面角D₁-EC-D的大小为

．若存在，确定点E的位置；若不存在，请说明理由．查看习题详情和答案>>

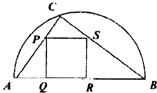如图，某小区准备绿化一块直径为AB的半圆形空地，点C在半圆弧上，半圆内△ABC外的地方种草，△ABC的内接正方形PQRS内部为一水池，其余地方种花，若AB=2a，∠CAB=θ，设△ABC的面积为S₁，正方形PQRS的边长为x，面积为S₂，将比值

称为“规划合理度”．
（1）求证：x=

．
（2）当a为定值，θ变化是，求“规划合理度”的最小值及此时角θ的大小．查看习题详情和答案>>

如图，已知△ABC中，∠C=

．设∠CBA=θ，BC=a，它的内接正方形DEFG的一边EF在斜边AB上，D、G分别在AC、BC上．假设△ABC的面积为S，正方形DEFG的面积为T．
（1）用a，θ表示△ABC的面积S和正方形DEFG的面积T；
（2）设f(θ)=

，试求f（θ）的最大值P，并判断此时△ABC的形状；
（3）通过对此题的解答，我们是否可以作如下推断：若需要从一块直角三角形的材料上裁剪一整块正方形（不得拼接），则这块材料的最大利用率要视该直角三角形的具体形状而定，但最大利用率不会超过第（2）小题中的结论P．请分析此推断是否正确，并说明理由．

查看习题详情和答案>>

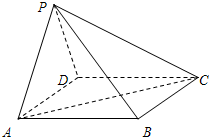如图，四棱锥P-ABCD的底面为矩形，侧面PAD是正三角形，且侧面PAD⊥底面ABCD
（I）求证：平面PAD⊥平面PCD
（II）试在平面PCD上确定一点 E 的位置，使|

|最小，并说明理由；
（III）当AD=AB时，求二面角A-PC-D的余弦值．

查看习题详情和答案>>

如图，在长方体中,，点在棱上移动，小蚂蚁从点沿长方体的表面经棱爬到点，所爬的最短路程为。

（1）求的长度；

（2）求证：⊥；w.w.w.k.s.5.u.c.o.m

（3）在线段上是否存在点，使得二面角的大小为。若存在，确定点的位置；若不存在，请说明理由。

查看习题详情和答案>>