摘要： 空间直线位置分三种:相交.平行.异面. 相交直线―共面有反且有一个公共点,平行直线―共面没有公共点,异面直线―不同在任一平面内[注]:①两条异面直线在同一平面内射影一定是相交的两条直线.(×)(可能两条直线平行.也可能是点和直线等)②直线在平面外.指的位置关系:平行或相交
网址：http://m.1010jiajiao.com/timu_id_490804[举报]
6、在平面上，两条直线的位置关系有相交、平行、重合三种．已知α，β是两个相交平面，空间两条直线l1，l2在α上的射影是直线S1，S2，l1，l2在β上的射影是直线t1，t2．用S1与S2，t1与t2的位置关系，写出一个总能确定l1与l2是异面直线的充分条件：
查看习题详情和答案>>
S1∥S2，并且t1与t2相交（或：t1∥t2，并且S1与S2相交）
．
10.在平面上，两条直线的位置关系有相交、平行、重合三种. 已知
是两个相交平面，空间两条直线l1、l2在
上的射影是直线s1、s2，l1、l2在
上的射影是直线t1、t2.用
与
，
与
的位置关系，写出一个总能确定
与
是异面直线的充分条件： .
查看习题详情和答案>>
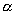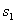是两个相交平面，空间两条直线l1、l2在上的射影是直线s1、s2，l1、l2在上的射影是直线t1、t2.用与，与的位置关系，写出一个总能确定与是异面直线的充分条件： .
查看习题详情和答案>>
在平面上，两条直线的位置关系有相交、平行、重合三种．已知α，β是两个相交平面，空间两条直线l1，l2在α上的射影是直线S1，S2，l1，l2在β上的射影是直线t1，t2．用S1与S2，t1与t2的位置关系，写出一个总能确定l1与l2是异面直线的充分条件： ．
查看习题详情和答案>>
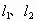在α上的射影是直线
，
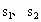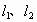在β上的射影是直线
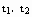．用
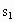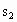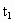与
，
与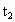
的位置关系，写出一个总能确定
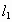与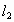
是异面直线的充分条件：_____________．