题目内容
在平面上,两条直线的位置关系有相交、平行、重合三种.已知α,β是两个相交平面,空间两条直线l1,l2在α上的射影是直线S1,S2,l1,l2在β上的射影是直线t1,t2.用S1与S2,t1与t2的位置关系,写出一个总能确定l1与l2是异面直线的充分条件: .
【答案】分析:由空间两条直线l1,l2在α上的射影是直线S1,S2,则当S1∥S2时,表示l1,l2平行或异面,而当S1与S2相交时,表示l1,l2相交或异面,故能确定l1与l2是异面直线的充分条件必然是l1,l2在α上的射影S1,S2,在β上的射影t1,t2.一组平行一组相交.
解答:解:∵当l1,l2异面时,l1,l2在α上的射影是直线S1,S2,可能平行或相交;
l1,l2在β上的射影是直线t1,t2,可能平行或相交;
但当直线S1∥S2与直线t1∥t2,同时成立时,则l1∥l2;
而当直线S1与S2、直线t1与t2,均相交时,则l1与l2与可能相交;
故能确定l1与l2是异面直线的充分条件是:S1∥S2,并且t1与t2相交(或:t1∥t2,并且S1与S2相交)
故答案:S1∥S2,并且t1与t2相交(或:t1∥t2,并且S1与S2相交)
点评:本题考查的知识点是异面直线的判断,及充要条件的判断,根据空间中线与面之间的关系,根据平行投影,我们对线面关系进行分类讨论,即可得到结论.
解答:解:∵当l1,l2异面时,l1,l2在α上的射影是直线S1,S2,可能平行或相交;
l1,l2在β上的射影是直线t1,t2,可能平行或相交;
但当直线S1∥S2与直线t1∥t2,同时成立时,则l1∥l2;
而当直线S1与S2、直线t1与t2,均相交时,则l1与l2与可能相交;
故能确定l1与l2是异面直线的充分条件是:S1∥S2,并且t1与t2相交(或:t1∥t2,并且S1与S2相交)
故答案:S1∥S2,并且t1与t2相交(或:t1∥t2,并且S1与S2相交)
点评:本题考查的知识点是异面直线的判断,及充要条件的判断,根据空间中线与面之间的关系,根据平行投影,我们对线面关系进行分类讨论,即可得到结论.

练习册系列答案
 冲刺100分1号卷系列答案
冲刺100分1号卷系列答案 期末好成绩系列答案
期末好成绩系列答案
相关题目
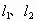 在α上的射影是直线
在α上的射影是直线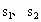 ,
,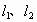 在β上的射影是直线
在β上的射影是直线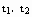 .用
.用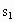 与
与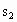 ,
,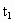 与
与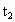 的位置关系,写出一个总能确定
的位置关系,写出一个总能确定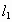 与
与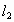 是异面直线的充分条件:_____________.
是异面直线的充分条件:_____________.