摘要：A.1 B. C.0 D.不存在
网址：http://m.1010jiajiao.com/timu_id_49058[举报]
一、选择题：本大题共10小题，每小题5分，共50分。在每小题给出的四个选项中，只有 一项是符合题目要求的。
题号
1
2
3
4
5
6
7
8
9
10
答案
二、填空题：（本大题共5个小题，每小题5分，共25分，）
11． 12. 13. 14. 15.
三、解答题：
已知A、D分别为椭圆E：
+
=1（a＞b＞0）的左顶点与上顶点，椭圆的离心率e=
，F1、F2为椭圆的左、右焦点，点P是线段AD上的任一点，且
．
的最大值为1．
（1）求椭圆E的方程．
（2）是否存在圆心在原点的圆，使得该圆的任意一条切线与椭圆E恒有两个交点A，B，且OA⊥OB（O为坐标原点），若存在，求出该圆的方程；若不存在，请说明理由．
（3）设直线l与圆C：x2+y2=R2（1＜R＜2）相切于A1，且l与椭圆E有且仅有一个公共点B1，当R为何值时，|A1B1|取最大值？并求最大值． 查看习题详情和答案>>
| x2 |
| a2 |
| y2 |
| b2 |
| ||
| 2 |
| PF1 |
| PF2 |
（1）求椭圆E的方程．
（2）是否存在圆心在原点的圆，使得该圆的任意一条切线与椭圆E恒有两个交点A，B，且OA⊥OB（O为坐标原点），若存在，求出该圆的方程；若不存在，请说明理由．
（3）设直线l与圆C：x2+y2=R2（1＜R＜2）相切于A1，且l与椭圆E有且仅有一个公共点B1，当R为何值时，|A1B1|取最大值？并求最大值． 查看习题详情和答案>>
已知A、B分别是直线y=
x和y=-
x上的两个动点，线段AB的长为2
，D是AB的中点．
（1）求动点D的轨迹C的方程；
（2）过点N（1，0）作与x轴不垂直的直线l，交曲线C于P、Q两点，若在线段ON上存在点M（m，0），使得以MP、MQ为邻边的平行四边形是菱形，试求m的取值范围． 查看习题详情和答案>>
| ||
| 3 |
| ||
| 3 |
| 3 |
（1）求动点D的轨迹C的方程；
（2）过点N（1，0）作与x轴不垂直的直线l，交曲线C于P、Q两点，若在线段ON上存在点M（m，0），使得以MP、MQ为邻边的平行四边形是菱形，试求m的取值范围． 查看习题详情和答案>>
和
上的两个动点，线段AB的长为
，D是AB的中点．
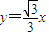和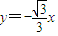
上的两个动点，线段AB的长为
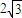，D是AB的中点．