题目内容
已知A、B分别是直线y=
| ||
| 3 |
| ||
| 3 |
| 3 |
(1)求动点D的轨迹C的方程;
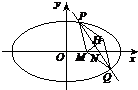
(2)过点N(1,0)作与x轴不垂直的直线l,交曲线C于P、Q两点,若在线段ON上存在点M(m,0),使得以MP、MQ为邻边的平行四边形是菱形,试求m的取值范围.
分析:(1)先设出D与A,B的坐标,用中点坐标公式把点D表示出来,再代入弦长公式即可得动点D的轨迹C的方程;
(2)把直线方程与轨迹C的方程联立求出与P、Q两点的坐标有关的等量关系,进而求出PQ的中点坐标,再利用菱形的对角线互相垂直即可求出m的取值范围.
(2)把直线方程与轨迹C的方程联立求出与P、Q两点的坐标有关的等量关系,进而求出PQ的中点坐标,再利用菱形的对角线互相垂直即可求出m的取值范围.
解答:解:(1)设D(x,y),A(x1,
x1),B(x2,-
x2).
∵D是线段AB的中点,∴x=
,y=
•
.(2分)
∵|AB|=2
,∴(x1-x2)2+(
x1+
x2)2=12,
∴(2
y)2+(
×2x)2=12.
化简得点D的轨迹C的方程为
+y2=1.(5分)
(2)设l:y=k(x-1)(k≠0),代入椭圆
+y2=1,得(1+9k2)x2-18k2x+9k2-9=0,∴x1+x2=
,∴y1+y2=
.(7分)
∴PQ中点H的坐标为(
,
).
∵以MP、MQ为邻边的平行四边形是菱形,∴kMH•k=-1,
 ∴
∴
•k=-1,即m=
.(9分)
∵k≠0,∴0<m<
.(11分)
又点M(m,0)在线段ON上,∴0<m<1.
综上,0<m<
.(12分)
| ||
| 3 |
| ||
| 3 |
∵D是线段AB的中点,∴x=
| x1+x2 |
| 2 |
| ||
| 3 |
| x1-x2 |
| 2 |
∵|AB|=2
| 3 |
| ||
| 3 |
| ||
| 3 |
∴(2
| 3 |
| ||
| 3 |
化简得点D的轨迹C的方程为
| x2 |
| 9 |
(2)设l:y=k(x-1)(k≠0),代入椭圆
| x2 |
| 9 |
| 18k2 |
| 1+9k2 |
| -2k |
| 1+9k2 |
∴PQ中点H的坐标为(
| 9k2 |
| 1+9k2 |
| -k |
| 1+9k2 |
∵以MP、MQ为邻边的平行四边形是菱形,∴kMH•k=-1,
 ∴
∴
| ||
|
| 8k2 |
| 1+9k2 |
∵k≠0,∴0<m<
| 8 |
| 9 |
又点M(m,0)在线段ON上,∴0<m<1.
综上,0<m<
| 8 |
| 9 |
点评:本小题主要考查直线与圆锥曲线的综合应用能力,具体涉及到轨迹方程的求法及直线与圆锥曲线的相关知识.

练习册系列答案
相关题目