摘要:由y=sinx的图象上的点的纵坐标保持不变.横坐标伸长或缩短到原来的倍.得到y=sinω x的图象.叫做周期变换或叫做沿x轴的伸缩变换.由y=sinx的图象上所有的点向左或向右平行移动|φ|个单位.得到y=sin的图象.叫做相位变换或叫做沿x轴方向的平移.由y=sinx的图象上所有的点向上平行移动|b|个单位.得到y=sinx+b的图象叫做沿y轴方向的平移.由y=sinx的图象利用图象变换作函数y=Asin的图象.要特别注意:当周期变换和相位变换的先后顺序不同时.原图象延x轴量伸缩量的区别.
网址:http://m.1010jiajiao.com/timu_id_490430[举报]
已知函数f(x)=sin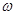 x(
x(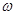 >0).
>0).
(1)若y=f(x)图象过点(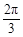 ,0),且在区间(0,
,0),且在区间(0,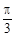 )上是增函数,求
)上是增函数,求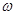 的值.
的值.
(2)先把(1)得到的函数y=f(x)图象上各点的纵坐标伸长为原来的2倍,(横坐标不变);再把所得的图象向右平移 个单位长度,设得到的图象所对应的函数为
个单位长度,设得到的图象所对应的函数为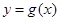 ,求当
,求当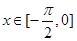 时,
时,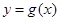 的最大和最小值
的最大和最小值
查看习题详情和答案>>
已知函数f(x)=sin x(
x( >0).
>0).
(1)若y=f(x)图象过点( ,0),且在区间(0,
,0),且在区间(0, )上是增函数,求
)上是增函数,求 的值.
的值.
(2)先把(1)得到的函数y=f(x)图象上各点的纵坐标伸长为原来的2倍,(横坐标不变);再把所得的图象向右平移 个单位长度,设得到的图象所对应的函数为
个单位长度,设得到的图象所对应的函数为 ,求当
,求当 时,
时, 的最大和最小值。
的最大和最小值。
查看习题详情和答案>>
已知函数f(x)=Asin(ωx+φ)(A>0,ω>0,0<φ<π)在x=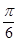 取得最大值2,且函数
取得最大值2,且函数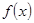 的最小正周期为2
的最小正周期为2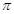 .现将函数y=f(x)图象上各点的横坐标缩小为原来的
.现将函数y=f(x)图象上各点的横坐标缩小为原来的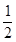 ,纵坐标不变,再把函数图像向右平移
,纵坐标不变,再把函数图像向右平移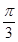 个单位,得到函数y=g(x)的图象,则
个单位,得到函数y=g(x)的图象,则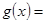
查看习题详情和答案>>
已知函数f(x)=2sin(2x+![]() ),将函数y=f(x)图象上各点的纵坐标保持不变,横坐标先缩短到原来的
),将函数y=f(x)图象上各点的纵坐标保持不变,横坐标先缩短到原来的![]() 倍,把所得图象再向左平移
倍,把所得图象再向左平移![]() 个单位,得到函数y=g(x)的图象,求y=g(x)在x∈[0,
个单位,得到函数y=g(x)的图象,求y=g(x)在x∈[0,![]() ]上的最小值.
]上的最小值.
函数y=3sin(2x+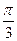 )的图象,可由y=sinx的图象经过下述哪种变换而得到:( )
)的图象,可由y=sinx的图象经过下述哪种变换而得到:( )
A.向右平移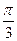 个单位,横坐标缩小到原来的 个单位,横坐标缩小到原来的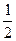 倍,纵坐标扩大到原来的3倍 倍,纵坐标扩大到原来的3倍 |
B.向左平移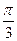 个单位,横坐标缩小到原来的 个单位,横坐标缩小到原来的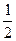 倍,纵坐标扩大到原来的3倍 倍,纵坐标扩大到原来的3倍 |
C.向右平移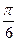 个单位,横坐标扩大到原来的2倍,纵坐标缩小到原来的 个单位,横坐标扩大到原来的2倍,纵坐标缩小到原来的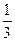 倍 倍 |
D.向左平移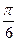 个单位,横坐标缩小到原来的 个单位,横坐标缩小到原来的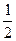 倍,纵坐标缩小到原来的 倍,纵坐标缩小到原来的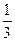 倍 倍 |