摘要: 三角函数的定义域:三角函数 定义域
网址:http://m.1010jiajiao.com/timu_id_490353[举报]
设函数f(x)对其定义域内的任意实数 ,则称函数f(x)为上凸函数. 若函数f(x)为上凸函数,则对定义域内任意x1、x2、x3,…,xn都有
,则称函数f(x)为上凸函数. 若函数f(x)为上凸函数,则对定义域内任意x1、x2、x3,…,xn都有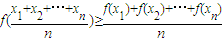 (当x1=x2=x3=…=xn时等号成立),称此不等式为琴生不等式,现有下列命题:
(当x1=x2=x3=…=xn时等号成立),称此不等式为琴生不等式,现有下列命题:
①f(x)=lnx(x>0)是上凸函数;
②二次函数f(x)=ax2+bx+c(a≠0)是上凸函数的充要条件是a>0;
③f(x)是上凸函数,若A(x1,f(x1)),B(x2,f(x2))是f(x)图象上任意两点,点C在线段AB上,且 ;
;
④设A,B,C是一个三角形的三个内角,则sinA+sinB+sinC的最大值是 .
.
其中,正确命题的序号是 (写出所有你认为正确命题的序号). 查看习题详情和答案>>
 ,则称函数f(x)为上凸函数. 若函数f(x)为上凸函数,则对定义域内任意x1、x2、x3,…,xn都有
,则称函数f(x)为上凸函数. 若函数f(x)为上凸函数,则对定义域内任意x1、x2、x3,…,xn都有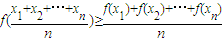 (当x1=x2=x3=…=xn时等号成立),称此不等式为琴生不等式,现有下列命题:
(当x1=x2=x3=…=xn时等号成立),称此不等式为琴生不等式,现有下列命题:①f(x)=lnx(x>0)是上凸函数;
②二次函数f(x)=ax2+bx+c(a≠0)是上凸函数的充要条件是a>0;
③f(x)是上凸函数,若A(x1,f(x1)),B(x2,f(x2))是f(x)图象上任意两点,点C在线段AB上,且
 ;
;④设A,B,C是一个三角形的三个内角,则sinA+sinB+sinC的最大值是
 .
.其中,正确命题的序号是 (写出所有你认为正确命题的序号). 查看习题详情和答案>>
设函数f(x)对其定义域内的任意实数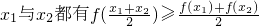 ,则称函数f(x)为上凸函数. 若函数f(x)为上凸函数,则对定义域内任意x1、x2、x3,…,xn都有
,则称函数f(x)为上凸函数. 若函数f(x)为上凸函数,则对定义域内任意x1、x2、x3,…,xn都有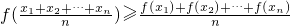 (当x1=x2=x3=…=xn时等号成立),称此不等式为琴生不等式,现有下列命题:
(当x1=x2=x3=…=xn时等号成立),称此不等式为琴生不等式,现有下列命题:
①f(x)=lnx(x>0)是上凸函数;
②二次函数f(x)=ax2+bx+c(a≠0)是上凸函数的充要条件是a>0;
③f(x)是上凸函数,若A(x1,f(x1)),B(x2,f(x2))是f(x)图象上任意两点,点C在线段AB上,且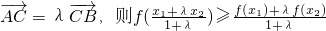 ;
;
④设A,B,C是一个三角形的三个内角,则sinA+sinB+sinC的最大值是 .
.
其中,正确命题的序号是________(写出所有你认为正确命题的序号).
查看习题详情和答案>>
设函数f(x)对其定义域内的任意实数x1与x2都有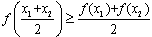 ,则称函数f(x)为上凸函数. 若函数f(x)为上凸函数,则对定义域内任意x1、x2、x3,…,xn都有
,则称函数f(x)为上凸函数. 若函数f(x)为上凸函数,则对定义域内任意x1、x2、x3,…,xn都有 (当x1=x2=x3=…=xn时等号成立),称此不等式为琴生不等式,现有下列命题:
(当x1=x2=x3=…=xn时等号成立),称此不等式为琴生不等式,现有下列命题:
①f(x)=lnx(x>0)是上凸函数;
②二次函数f(x)=ax2+bx+c(a≠0)是上凸函数的充要条件是a>0;
③f(x)是上凸函数,若A(x1,f(x1)),B(x2,f(x2))是f(x)图象上任意两点,点C在线段AB上,且 ,则
,则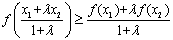 ;
;
④设A,B,C是一个三角形的三个内角,则sinA+sinB+sinC的最大值是 .
.
其中,正确命题的序号是( )(写出所有你认为正确命题的序号).
查看习题详情和答案>>
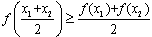 ,则称函数f(x)为上凸函数. 若函数f(x)为上凸函数,则对定义域内任意x1、x2、x3,…,xn都有
,则称函数f(x)为上凸函数. 若函数f(x)为上凸函数,则对定义域内任意x1、x2、x3,…,xn都有 (当x1=x2=x3=…=xn时等号成立),称此不等式为琴生不等式,现有下列命题:
(当x1=x2=x3=…=xn时等号成立),称此不等式为琴生不等式,现有下列命题:①f(x)=lnx(x>0)是上凸函数;
②二次函数f(x)=ax2+bx+c(a≠0)是上凸函数的充要条件是a>0;
③f(x)是上凸函数,若A(x1,f(x1)),B(x2,f(x2))是f(x)图象上任意两点,点C在线段AB上,且
 ,则
,则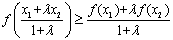 ;
;④设A,B,C是一个三角形的三个内角,则sinA+sinB+sinC的最大值是
 .
.其中,正确命题的序号是( )(写出所有你认为正确命题的序号).
对于函数y=f(x),x∈(0,+∞),如果a,b,c是一个三角形的三边长,那么f(a),f(b),f(c)也是一个三角形的三边长,则称函数f(x)为“保三角形函数”.
对于函数y=g(x),x∈[0,+∞),如果a,b,c是任意的非负实数,都有g(a),g(b),g(c)是一个三角形的三边长,则称函数g(x)为“恒三角形函数”.
(Ⅰ)判断三个函数“f1(x)=x,f2(x)=
,f3(x)=3x2(定义域均为x∈(0,+∞))”中,哪些是“保三角形函数”?请说明理由;
(Ⅱ)若函数g(x)=
,x∈[{0,+∞})是“恒三角形函数”,试求实数k的取值范围;
(Ⅲ)如果函数h(x)是定义在(0,+∞)上的周期函数,且值域也为(0,+∞),试证明:h(x)既不是“恒三角形函数”,也不是“保三角形函数”. 查看习题详情和答案>>
对于函数y=g(x),x∈[0,+∞),如果a,b,c是任意的非负实数,都有g(a),g(b),g(c)是一个三角形的三边长,则称函数g(x)为“恒三角形函数”.
(Ⅰ)判断三个函数“f1(x)=x,f2(x)=
| 2x |
(Ⅱ)若函数g(x)=
| x2+kx+1 |
| x2-x+1 |
(Ⅲ)如果函数h(x)是定义在(0,+∞)上的周期函数,且值域也为(0,+∞),试证明:h(x)既不是“恒三角形函数”,也不是“保三角形函数”. 查看习题详情和答案>>