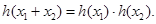摘要: 数列常见的几种形式:
网址:http://m.1010jiajiao.com/timu_id_490307[举报]
(2010•绵阳二模)已知数列{an}满足:an=logn+1(n+2),n∈N*,我们把使a1•a2•…•ak为整数的数k(k∈N*)叫做数列{an}的理想数.给出下列关于数列{an}的几个结论:
①数列{an}的最小理想数是2.
②{an}的理想数k的形式可以表示为k=4n-2(n∈N*).
③对任意n∈N*,有an+1<an.
④
an=0.
其中正确结论的序号为
查看习题详情和答案>>
①数列{an}的最小理想数是2.
②{an}的理想数k的形式可以表示为k=4n-2(n∈N*).
③对任意n∈N*,有an+1<an.
④
| lim | n→+∞ |
其中正确结论的序号为
①③
①③
.12、在中学数学中,从特殊到一般,从具体到抽象是常见的一种思维形式如从f(x)=lgx可抽象出f(x1•x2)=f(x1)+f(x2)的性质,那么由h(x)=
查看习题详情和答案>>
任意指数函数均可,如h(x)=2x
(填一个具体的函数)可抽象出性质h(x1+x2)=h(x1)•h(x2).已知f(x)=lgx:
(1)在中学数学中,从特殊到一般,从具体到抽象是常见的一种思维形式,如从f(x)=lgx可抽象出性质:f(x1•x2)=f(x1)+f(x2).
对于下面两个具体函数,试分别抽象出一个与上面类似的性质:
由h(x)=2x可抽象出性质为
由φ(x)=3x+1可抽象出性质为
(2)g(x)=f(x2+6x+4)-f(x),求g(x)的最小值.
查看习题详情和答案>>
(1)在中学数学中,从特殊到一般,从具体到抽象是常见的一种思维形式,如从f(x)=lgx可抽象出性质:f(x1•x2)=f(x1)+f(x2).
对于下面两个具体函数,试分别抽象出一个与上面类似的性质:
由h(x)=2x可抽象出性质为
h(x1+x2)=h(x1)•h(x2)
h(x1+x2)=h(x1)•h(x2)
,由φ(x)=3x+1可抽象出性质为
φ(x1+x2)=φ(x1)+φ(x2)
φ(x1+x2)=φ(x1)+φ(x2)
.(2)g(x)=f(x2+6x+4)-f(x),求g(x)的最小值.
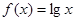 可抽象出
可抽象出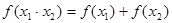 的性质,那么由
的性质,那么由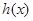 = (填一个具体的函数)可抽象出性质
= (填一个具体的函数)可抽象出性质