摘要： 常用公式:①1+2+3 -+n =
网址：http://m.1010jiajiao.com/timu_id_490296[举报]
21.某公司全年的纯利润为b元，其中一部分作为奖金发给n位职工.奖金分配方案如下：首先将职工按工作业绩（工作业绩均不相同）从大到小.由1至n排序，第1位职工得奖金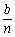
元，然后再将余额除以n发给第2位职工，按此方法将奖金逐一发给每位职工.并将最后剩余部分作为公司发展基金.
元，然后再将余额除以n发给第2位职工，按此方法将奖金逐一发给每位职工.并将最后剩余部分作为公司发展基金.
（1）设ak（1≤k≤n）为第k位职工所得奖金额，试求a2、a3，并用k、n和b表示ak ；（不必证明）
（2）证明a k＞a k＋1(k＝1，2，…，n－1)，并解释此不等式关于分配原则的实际意义；
（3）发展基金与n和b有关，记为Pn（b）.对常数b，当n变化时，求
Pn（b）.
（1）选修4-2：矩阵与变换
若二阶矩阵M满足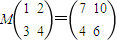
．
（Ⅰ）求二阶矩阵M；
（Ⅱ）把矩阵M所对应的变换作用在曲线3x2+8xy+6y2=1上，求所得曲线的方程．
（2）选修4-4：坐标系与参数方程
已知在直角坐标系xOy中，曲线C的参数方程为
（t为非零常数，θ为参数），在极坐标系（与直角坐标系xOy取相同的长度单位，且以原点O为极点，以x轴正半轴为极轴）中，直线l的方程为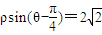
．
（Ⅰ）求曲线C的普通方程并说明曲线的形状；
（Ⅱ）是否存在实数t，使得直线l与曲线C有两个不同的公共点A、B，且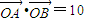
（其中O为坐标原点）？若存在，请求出；否则，请说明理由．
（3）选修4-5：不等式选讲
已知函数f（x）=|x-2|+|x-4|的最小值为m，实数a，b，c，n，p，q满足a2+b2+c2=n2+p2+q2=m．
（Ⅰ）求m的值；
（Ⅱ）求证：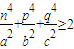
．
查看习题详情和答案>>
若二阶矩阵M满足
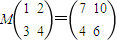．（Ⅰ）求二阶矩阵M；
（Ⅱ）把矩阵M所对应的变换作用在曲线3x2+8xy+6y2=1上，求所得曲线的方程．
（2）选修4-4：坐标系与参数方程
已知在直角坐标系xOy中，曲线C的参数方程为
（t为非零常数，θ为参数），在极坐标系（与直角坐标系xOy取相同的长度单位，且以原点O为极点，以x轴正半轴为极轴）中，直线l的方程为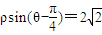．（Ⅰ）求曲线C的普通方程并说明曲线的形状；
（Ⅱ）是否存在实数t，使得直线l与曲线C有两个不同的公共点A、B，且
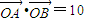（其中O为坐标原点）？若存在，请求出；否则，请说明理由．（3）选修4-5：不等式选讲
已知函数f（x）=|x-2|+|x-4|的最小值为m，实数a，b，c，n，p，q满足a2+b2+c2=n2+p2+q2=m．
（Ⅰ）求m的值；
（Ⅱ）求证：
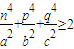．查看习题详情和答案>>
某公司全年的利润为b元，其中一部分作为奖金发给n位职工，奖金分配方案如下：首先将职工按工作业绩(工作业绩均不相同)从大到小，由1到n排序，第一位职工得奖金
元，然后再将余额除以n发给第2位职工，按此方法将奖金逐一发给每位职工，并将最后剩余部分作为公司发展基金．
(1)设ak(1≤k≤n)为第k位职工所得奖金额，试求a2、a3，并用k、n和b表示ak(不必证明)；
(2)证明ak＞ak+1(k＝1，2，…，n－1)，并解释此不等式关于分配原则的实际意义；
(3)发展基金与n和b有关，记为Pn(b)，对常数b，当n变化时，求
Pn(b)
元，然后再将余额除以n发给第2位职工，按此方法将奖金逐一发给每位职工，并将最后剩余部分作为公司发展基金．
Pn(b)．
×100％，各种类型家庭的n如下表所示：