摘要:从而.又平面.
网址:http://m.1010jiajiao.com/timu_id_489559[举报]
如图,在四棱锥 中,
中, ⊥底面
⊥底面 ,底面
,底面 为正方形,
为正方形, ,
, ,
, 分别是
分别是 ,
, 的中点.
的中点.
(I)求证: 平面
平面 ;
;
(II)求证: ;
;
(III)设PD=AD=a, 求三棱锥B-EFC的体积.

【解析】第一问利用线面平行的判定定理, ,得到
,得到
第二问中,利用
 ,所以
,所以
又因为 ,
, ,从而得
,从而得
第三问中,借助于等体积法来求解三棱锥B-EFC的体积.
(Ⅰ)证明:
 分别是
分别是 的中点,
的中点, 
 ,
, . …4分
. …4分
(Ⅱ)证明: 四边形
四边形 为正方形,
为正方形, .
.
 ,
,  .
.
 ,
,  ,
,
 .
. ,
, . ………8分
. ………8分
(Ⅲ)解:连接AC,DB相交于O,连接OF, 则OF⊥面ABCD,
∴

查看习题详情和答案>>
某公园里有一造型别致的小屋,其墙面与水平面所成的角为θ,小屋有一扇面向正南的窗户,现要在窗户的上方搭建一个与水平面平行的遮阳篷,如图1所示.如图2是遮阳篷的截面示意图,AB表示窗户上、下边框的距离,AB=m,CD表示遮阳篷.已知该公园夏季正午太阳最高这一天,太阳光线与水平面所成角为α,冬季正午太阳最低这一天,太阳光线与水平面所成角为β(α>β).若要使得夏季正午太阳最高这一天太阳光线不从窗户直射进室内,而冬季正午太阳最低这一天太阳光线又恰能最大限度地直射进室内,那么遮阳篷的伸出长度CD和遮阳篷与窗户上边框的距离BC各为多少?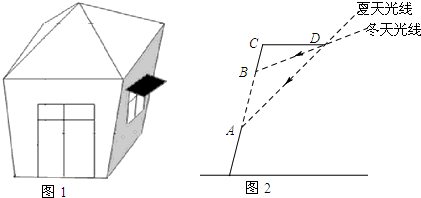
查看习题详情和答案>>
某公园里有一造型别致的小屋,其墙面与水平面所成的角为θ,小屋有一扇面向正南的窗户,现要在窗户的上方搭建一个与水平面平行的遮阳篷,如图1所示.如图2是遮阳篷的截面示意图,AB表示窗户上、下边框的距离,AB=m,CD表示遮阳篷.已知该公园夏季正午太阳最高这一天,太阳光线与水平面所成角为α,冬季正午太阳最低这一天,太阳光线与水平面所成角为β(α>β).若要使得夏季正午太阳最高这一天太阳光线不从窗户直射进室内,而冬季正午太阳最低这一天太阳光线又恰能最大限度地直射进室内,那么遮阳篷的伸出长度CD和遮阳篷与窗户上边框的距离BC各为多少?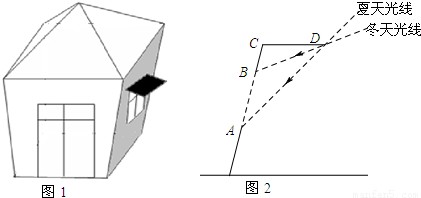
查看习题详情和答案>>

查看习题详情和答案>>