网址:http://m.1010jiajiao.com/timu_id_487558[举报]
1.D 2.AD 3.BD 4.D 5. C 6.AD 7.B 8.AD 9.AD 10.B
11. 100J 75J 12. 15N
13. 解:设卡车运动的速度为v0,刹车后至停止运动,由动能定理:-μmgs=0-动能定理与能量守恒.files/image345.gif) 。得v=
。得v=动能定理与能量守恒.files/image347.gif) =
=
14. 解:当人向右匀速前进的过程中,绳子与竖直
方向的夹角由0°逐渐增大,人的拉力就发生了变化,
故无法用W=Fscosθ计算拉力所做的功,而在这个过
动能定理与能量守恒.files/image348.gif) 程中,人的拉力对物体做的功使物体的动能发生了变
程中,人的拉力对物体做的功使物体的动能发生了变
化,故可以用动能定理来计算拉力做的功。
当人在滑轮的正下方时,物体的初速度为零,
当人水平向右匀速前进s 时物体的速度为v1 ,由图
1可知: v1= v0sina
⑴根据动能定理,人的拉力对物体所做的功
W=m v12/2-0
⑵由⑴、⑵两式得W=ms2 v12/2(s2+h2)
15. 解:(1)对AB段应用动能定理:mgR+Wf=动能定理与能量守恒.files/image350.gif)
所以:Wf=动能定理与能量守恒.files/image350.gif) -mgR=
-mgR=动能定理与能量守恒.files/image353.gif) -20×10-3×10×1=-0.11J
-20×10-3×10×1=-0.11J
(2)对BC段应用动能定理:Wf=0-动能定理与能量守恒.files/image350.gif) =-
=-动能定理与能量守恒.files/image353.gif) =-0.09J。又因Wf=μmgBCcos1800=-0.09,得:μ=0.153。
=-0.09J。又因Wf=μmgBCcos1800=-0.09,得:μ=0.153。
16. 解:在此过程中,B的重力势能的增量为动能定理与能量守恒.files/image355.gif) ,A、B动能增量为
,A、B动能增量为动能定理与能量守恒.files/image357.gif) ,恒力F所做的功为
,恒力F所做的功为动能定理与能量守恒.files/image359.gif) ,用
,用动能定理与能量守恒.files/image361.gif) 表示A克服摩擦力所做的功,根据功能关系有:
表示A克服摩擦力所做的功,根据功能关系有:
动能定理与能量守恒.files/image363.gif)
解得:动能定理与能量守恒.files/image365.gif)
17. 解:(1)儿童从A点滑到E点的过程中,重力做功W=mgh
儿童由静止开始滑下最后停在E点,在整个过程中克服摩擦力做功W1,由动能定理得,
动能定理与能量守恒.files/image367.gif) =0,则克服摩擦力做功为W1=mgh
=0,则克服摩擦力做功为W1=mgh
(2)设斜槽AB与水平面的夹角为动能定理与能量守恒.files/image369.gif) ,儿童在斜槽上受重力mg、支持力N1和滑动摩擦
,儿童在斜槽上受重力mg、支持力N1和滑动摩擦
力f1,动能定理与能量守恒.files/image371.gif) ,儿童在水平槽上受重力mg、支持力N2和滑动摩擦力f2,
,儿童在水平槽上受重力mg、支持力N2和滑动摩擦力f2,
动能定理与能量守恒.files/image373.gif) ,儿童从A点由静止滑下,最后停在E点.
,儿童从A点由静止滑下,最后停在E点.
由动能定理得,动能定理与能量守恒.files/image375.gif)
解得动能定理与能量守恒.files/image377.gif) ,它与角
,它与角动能定理与能量守恒.files/image379.gif) 无关.
无关.
(3)儿童沿滑梯滑下的过程中,通过B点的速度最大,显然,倾角动能定理与能量守恒.files/image381.gif) 越大,通过B点的速度越大,设倾角为
越大,通过B点的速度越大,设倾角为动能定理与能量守恒.files/image383.gif) 时有最大速度v,由动能定理得,
时有最大速度v,由动能定理得,
动能定理与能量守恒.files/image385.gif)
解得最大倾角动能定理与能量守恒.files/image387.gif)
18.
解:(1)根据牛顿第二定律有:动能定理与能量守恒.files/image389.gif)
设匀加速的末速度为动能定理与能量守恒.files/image063.gif) ,则有:
,则有:动能定理与能量守恒.files/image392.gif) 、
、动能定理与能量守恒.files/image394.gif)
代入数值,联立解得:匀加速的时间为:动能定理与能量守恒.files/image396.gif)
(2)当达到最大速度动能定理与能量守恒.files/image087.gif) 时,有:
时,有:动能定理与能量守恒.files/image399.gif)
解得:汽车的最大速度为:动能定理与能量守恒.files/image401.gif)
(3)汽车匀加速运动的位移为:动能定理与能量守恒.files/image403.gif)
在后一阶段牵引力对汽车做正功,重力和阻力做负功,根据动能定理有:
动能定理与能量守恒.files/image405.gif)
又有动能定理与能量守恒.files/image407.gif)
代入数值,联立求解得:动能定理与能量守恒.files/image409.gif)
所以汽车总的运动时间为:动能定理与能量守恒.files/image411.gif)

(1)要使滑块与箱子这一系统损耗的总动能不超过其初始动能的50%,滑块与箱壁最多可碰撞几次?
(2)从滑块开始运动到滑块与箱壁刚完成第三次碰撞的期间,箱子克服摩擦力做功的平均功率是多少?
(
| 2 |
| 3 |
| 5 |
| 10 |
(1)要使滑块与箱子这一系统损耗的总动能不超过其初始动能的50%,滑块与箱壁最多可碰撞几次?
(2)从滑块开始运动到滑块与箱壁刚完成第三次碰撞的期间,箱子克服摩擦力做功的平均功率是多少?
(
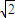 =1.414,
=1.414,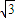 =1.732,
=1.732,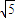 =2.236,
=2.236,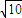 3=.162)
3=.162) 查看习题详情和答案>>
查看习题详情和答案>>
(1)若该人在踏板上保持站式,由伙伴将其推至摆角θ弧度,由静止释放,忽略空气阻力,求摆至最低点时绳中的拉力大小;
(2)若该人在踏板上保持站式,由伙伴将其推至摆角θ1弧度,由静止释放,摆至另一侧最大摆角为θ2弧度,设空气阻力大小恒定,作用点距离脚底为H/3,求空气阻力的大小.
(3)若该人在踏板上采取如下步骤:当荡至最高处时,突然由蹲式迅速站起,而后缓缓蹲下,摆至另一侧最高处时已是蹲式,在该处又迅速站起,之后不断往复,可以荡起很高.记此法可以荡起的最大摆角为θm 弧度,假设人的“缓缓蹲下”这个动作不会导致系统机械能的损耗,而且空气阻力大小和作用点与第(2)问相同,试证明:
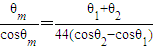 .
. 查看习题详情和答案>>
查看习题详情和答案>>
 荡秋千是一项古老的运动,设某人的质量为m,身高为H,站立时重心离脚底H/2,蹲下时重心离脚底H/4,绳子悬挂点到踏板的绳长为6H,绳子足够柔软且不可伸长,绳子和踏板的质量不计,人身体始终与绳子保持平行,重力加速度为g.
荡秋千是一项古老的运动,设某人的质量为m,身高为H,站立时重心离脚底H/2,蹲下时重心离脚底H/4,绳子悬挂点到踏板的绳长为6H,绳子足够柔软且不可伸长,绳子和踏板的质量不计,人身体始终与绳子保持平行,重力加速度为g.(1)若该人在踏板上保持站式,由伙伴将其推至摆角θ0弧度,由静止释放,忽略空气阻力,求摆至最低点时绳中的拉力大小;
(2)若该人在踏板上保持站式,由伙伴将其推至摆角θ1弧度,由静止释放,摆至另一侧最大摆角为θ2弧度,设空气阻力大小恒定,作用点距离脚底为H/3,求空气阻力的大小.
(3)若该人在踏板上采取如下步骤:当荡至最高处时,突然由蹲式迅速站起,而后缓缓蹲下,摆至另一侧最高处时已是蹲式,在该处又迅速站起,之后不断往复,可以荡起很高.记此法可以荡起的最大摆角为θm 弧度,假设人的“缓缓蹲下”这个动作不会导致系统机械能的损耗,而且空气阻力大小和作用点与第(2)问相同,试证明:
| θm |
| cosθm |
| θ1+θ2 |
| 44(cosθ2-cosθ1) |
荡秋千是一项古老的运动,秋千是一块板用两根绳系在两个固定的悬点组成,设某人的质量为m,身高为H,站立时重心离脚底H/2,蹲下时重心离脚底H/4,绳子悬挂点到踏板的绳长为6H,绳子足够柔软且不可伸长,绳子和踏板的质量不计,人身体始终与绳子保持平行,重力加速度为g。
1.若该人在踏板上保持站式,由伙伴将其推至摆角θ0(单位:rad),由静止释放,忽略空气阻力,求摆至最低点时每根绳的拉力大小;
2.若该人在踏板上保持站式,由伙伴将其推至摆角θ1 (单位:rad),由静止释放,摆至另一侧最大摆角为θ2(单位:rad),设空气阻力大小恒定,作用点距离脚底为H/3,求空气阻力的大小。
3.若该人在踏板上采取如下步骤:当荡至最高处时,突然由蹲式迅速站起,而后缓缓蹲下,摆至另一侧最高处时已是蹲式,在该处又迅速站起,之后不断往复,可以荡起很高。用此法可以荡起的最大摆角为θm 弧度,假设人的“缓缓蹲下”这个动作不会导致系统机械能的损耗,而且空气阻力大小和作用点与第(2)问相同,试证明:。
查看习题详情和答案>>