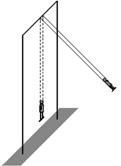
题目内容
荡秋千是一项古老的运动,秋千是一块板用两根绳系在两个固定的悬点组成,设某人的质量为m,身高为H,站立时重心离脚底H/2,蹲下时重心离脚底H/4,绳子悬挂点到踏板的绳长为6H,绳子足够柔软且不可伸长,绳子和踏板的质量不计,人身体始终与绳子保持平行,重力加速度为g。
1.若该人在踏板上保持站式,由伙伴将其推至摆角θ0(单位:rad),由静止释放,忽略空气阻力,求摆至最低点时每根绳的拉力大小;
2.若该人在踏板上保持站式,由伙伴将其推至摆角θ1 (单位:rad),由静止释放,摆至另一侧最大摆角为θ2(单位:rad),设空气阻力大小恒定,作用点距离脚底为H/3,求空气阻力的大小。
3.若该人在踏板上采取如下步骤:当荡至最高处时,突然由蹲式迅速站起,而后缓缓蹲下,摆至另一侧最高处时已是蹲式,在该处又迅速站起,之后不断往复,可以荡起很高。用此法可以荡起的最大摆角为θm 弧度,假设人的“缓缓蹲下”这个动作不会导致系统机械能的损耗,而且空气阻力大小和作用点与第(2)问相同,试证明:。
1.![]()
2.![]()
3.见解析
解析:(1)设荡至最低点时速度为v,则由机械能守恒定律有 设拉力为F,则由牛顿第二定律
求得 ![]()
每根绳的拉力 ![]()
(2)全程损耗的机械能为 空气阻力做的功为
由功能关系有
求得 ![]()
(3)在一个周期内,通过“迅速站起”获得的机械能(重力势能)是
空气阻力做的功是
由功能关系有
求得 ,得证。

 口算心算速算应用题系列答案
口算心算速算应用题系列答案 同步拓展阅读系列答案
同步拓展阅读系列答案 荡秋千是一项古老的运动,设某人的质量为m,身高为H,站立时重心离脚底H/2,蹲下时重心离脚底H/4,绳子悬挂点到踏板的绳长为6H,绳子足够柔软且不可伸长,绳子和踏板的质量不计,人身体始终与绳子保持平行,重力加速度为g.
荡秋千是一项古老的运动,设某人的质量为m,身高为H,站立时重心离脚底H/2,蹲下时重心离脚底H/4,绳子悬挂点到踏板的绳长为6H,绳子足够柔软且不可伸长,绳子和踏板的质量不计,人身体始终与绳子保持平行,重力加速度为g. 。
。
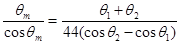 。
。