摘要:∴ 可以看出等式左边是偶数右边是奇数.∴假设不成立.∴数列中不存在三项.它们可以构成等差数列.----10分
网址:http://m.1010jiajiao.com/timu_id_486631[举报]
已知 是公差为d的等差数列,
是公差为d的等差数列, 是公比为q的等比数列
是公比为q的等比数列
(Ⅰ)若  ,是否存在
,是否存在 ,有
,有 ?请说明理由;
?请说明理由;
(Ⅱ)若 (a、q为常数,且aq
(a、q为常数,且aq 0)对任意m存在k,有
0)对任意m存在k,有 ,试求a、q满足的充要条件;
,试求a、q满足的充要条件;
(Ⅲ)若 试确定所有的p,使数列
试确定所有的p,使数列 中存在某个连续p项的和式数列中
中存在某个连续p项的和式数列中 的一项,请证明.
的一项,请证明.
【解析】第一问中,由 得
得 ,整理后,可得
,整理后,可得
 、
、 ,
, 为整数
为整数 不存在
不存在 、
、 ,使等式成立。
,使等式成立。
(2)中当 时,则
时,则
 即
即 ,其中
,其中 是大于等于
是大于等于 的整数
的整数
反之当 时,其中
时,其中 是大于等于
是大于等于 的整数,则
的整数,则 ,
,
显然 ,其中
,其中

 、
、 满足的充要条件是
满足的充要条件是 ,其中
,其中 是大于等于
是大于等于 的整数
的整数
(3)中设 当
当 为偶数时,
为偶数时, 式左边为偶数,右边为奇数,
式左边为偶数,右边为奇数,
当 为偶数时,
为偶数时, 式不成立。由
式不成立。由 式得
式得 ,整理
,整理
当 时,符合题意。当
时,符合题意。当 ,
, 为奇数时,
为奇数时,
结合二项式定理得到结论。
解(1)由 得
得 ,整理后,可得
,整理后,可得
 、
、 ,
, 为整数
为整数 不存在
不存在 、
、 ,使等式成立。
,使等式成立。
(2)当 时,则
时,则
 即
即 ,其中
,其中 是大于等于
是大于等于 的整数反之当
的整数反之当 时,其中
时,其中 是大于等于
是大于等于 的整数,则
的整数,则 ,
,
显然 ,其中
,其中

 、
、 满足的充要条件是
满足的充要条件是 ,其中
,其中 是大于等于
是大于等于 的整数
的整数
(3)设 当
当 为偶数时,
为偶数时, 式左边为偶数,右边为奇数,
式左边为偶数,右边为奇数,
当 为偶数时,
为偶数时, 式不成立。由
式不成立。由 式得
式得 ,整理
,整理
当 时,符合题意。当
时,符合题意。当 ,
, 为奇数时,
为奇数时,

 由
由 ,得
,得

 当
当 为奇数时,此时,一定有
为奇数时,此时,一定有 和
和 使上式一定成立。
使上式一定成立。 当
当 为奇数时,命题都成立
为奇数时,命题都成立
查看习题详情和答案>>
(2009•黄冈模拟)下列说法中正确的是( )
①命题:“a、b都是奇数,则a+b是偶数”的逆否命题是“a+b不是偶数,则a、b不都是奇数”;
②若等式sin(α+β)=sinα+sinβ对任意角β都成立,则角α可以是2π;
③若a<0,-1<b<0,则ab>a>ab2;
④椭圆
+
=1上一点P到左焦点的距离等于3,则P到右准线的距离是5.
①命题:“a、b都是奇数,则a+b是偶数”的逆否命题是“a+b不是偶数,则a、b不都是奇数”;
②若等式sin(α+β)=sinα+sinβ对任意角β都成立,则角α可以是2π;
③若a<0,-1<b<0,则ab>a>ab2;
④椭圆
| x2 |
| 25 |
| y2 |
| 16 |
查看习题详情和答案>>
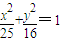 上一点P到左焦点的距离等于3,则P到右准线的距离是5.
上一点P到左焦点的距离等于3,则P到右准线的距离是5.