题目内容
下列说法中正确的是( )①命题:“a、b都是奇数,则a+b是偶数”的逆否命题是“a+b不是偶数,则a、b不都是奇数”;
②若等式sin(α+β)=sinα+sinβ对任意角β都成立,则角α可以是2π;
③若a<0,-1<b<0,则ab>a>ab2;
④椭圆
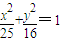 上一点P到左焦点的距离等于3,则P到右准线的距离是5.
上一点P到左焦点的距离等于3,则P到右准线的距离是5.A.①②
B.②③
C.②④
D.③④
【答案】分析:①原命题的逆否命题是先否定原命题的题设做结论,再否定原命题的结论做题设,即可得到原命题的逆否命题.
②当α=2π时,代入已知可得②正确.
③利用特值法,取a=-1,b=- ,则ab>a>ab2不成立.
,则ab>a>ab2不成立.
④根据题意并且结合椭圆的定义可得:椭圆的点P到右焦点的距离等于7,由椭圆的第二定义可得答案.
解答:解:①因为“a,b都是奇数”的否命题是“a,b不都是奇数”,“a+b是偶数”的否命题是“a+b不是偶数”,
所以原命题的逆否命题是“若a+b不是偶数,则a,b不都是奇数”,所以①正确.
②当α=2π时,sin(α+β)=sin(2π+β)=sin2π+sinβ=sinα+sinβ,所以②正确.
③因为a<0,-1<b<0,所以取a=-1,b=- ,则ab>a>ab2不成立,所以③错误.
,则ab>a>ab2不成立,所以③错误.
④根据题意并且结合椭圆的定义可得:椭圆的点P到右焦点的距离等于7,由椭圆的第二定义可得:P到右准线的距离是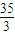 ,所以④错误.
,所以④错误.
故选A.
点评:解决此类问题的关键是熟练掌握椭圆的定义与第二定义、不等式的基本性质、三角的有关公式,以及四种命题之间的关系等知识点,此类题目考查的知识点比较基础,但是容易出错,在解决此类问题时要认真仔细,并且熟练掌握有关的知识点.
②当α=2π时,代入已知可得②正确.
③利用特值法,取a=-1,b=-
 ,则ab>a>ab2不成立.
,则ab>a>ab2不成立.④根据题意并且结合椭圆的定义可得:椭圆的点P到右焦点的距离等于7,由椭圆的第二定义可得答案.
解答:解:①因为“a,b都是奇数”的否命题是“a,b不都是奇数”,“a+b是偶数”的否命题是“a+b不是偶数”,
所以原命题的逆否命题是“若a+b不是偶数,则a,b不都是奇数”,所以①正确.
②当α=2π时,sin(α+β)=sin(2π+β)=sin2π+sinβ=sinα+sinβ,所以②正确.
③因为a<0,-1<b<0,所以取a=-1,b=-
 ,则ab>a>ab2不成立,所以③错误.
,则ab>a>ab2不成立,所以③错误.④根据题意并且结合椭圆的定义可得:椭圆的点P到右焦点的距离等于7,由椭圆的第二定义可得:P到右准线的距离是
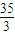 ,所以④错误.
,所以④错误.故选A.
点评:解决此类问题的关键是熟练掌握椭圆的定义与第二定义、不等式的基本性质、三角的有关公式,以及四种命题之间的关系等知识点,此类题目考查的知识点比较基础,但是容易出错,在解决此类问题时要认真仔细,并且熟练掌握有关的知识点.

练习册系列答案
 口算心算速算应用题系列答案
口算心算速算应用题系列答案 同步拓展阅读系列答案
同步拓展阅读系列答案
相关题目