摘要：(Ⅲ)在线段AC上是否存在一点M使得直线BM与平面所成角为.证明:
网址：http://m.1010jiajiao.com/timu_id_484870[举报]
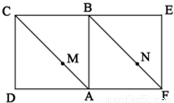
（2013•西城区一模）在如图所示的几何体中，面CDEF为正方形，面ABCD为等腰梯形，AB∥CD，AC=| 3 |
（Ⅰ）求证：AC⊥平面FBC；
（Ⅱ）求四面体FBCD的体积；
（Ⅲ）线段AC上是否存在点M，使EA∥平面FDM？证明你的结论．
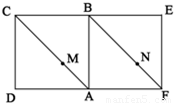
如图，平面内两正方形ABCD与ABEF，点M、N分别在对角线AC、FB上，且AM：MC=FN：NB，沿AB折成直二面角．（1）证明：折叠后MN∥平面CBE；
（2）若AM：MC=2：3，在线段AB上是否存在一点G，使平面MGN∥平面CBE？若存在，试确定点G的位置．
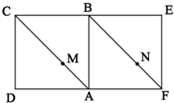
如图，平面内两正方形ABCD与ABEF，点M、N分别在对角线AC、FB上，且AM：MC=FN：NB，沿AB折成直二面角．
（1）证明：折叠后MN∥平面CBE；
（2）若AM：MC=2：3，在线段AB上是否存在一点G，使平面MGN∥平面CBE？若存在，试确定点G的位置．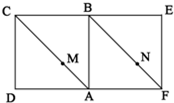
查看习题详情和答案>>
（1）证明：折叠后MN∥平面CBE；
（2）若AM：MC=2：3，在线段AB上是否存在一点G，使平面MGN∥平面CBE？若存在，试确定点G的位置．
