题目内容
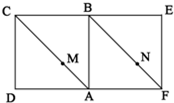
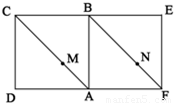
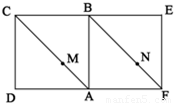
如图,平面内两正方形ABCD与ABEF,点M、N分别在对角线AC、FB上,且AM:MC=FN:NB,沿AB折成直二面角.(1)证明:折叠后MN∥平面CBE;
(2)若AM:MC=2:3,在线段AB上是否存在一点G,使平面MGN∥平面CBE?若存在,试确定点G的位置.
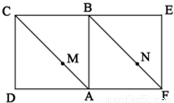
【答案】分析:(1)在AB上取一点G,使AG:GB=AM:MC=FN:NB,则MG∥BC,NG∥BE,从而平面MNG∥平面CBE,由此能够证明MN∥平面CBE.
(2)由(1)知,当AG:GB=AM:MC=FN:NB=2:3时,平面MGN∥平面CBE.
解答:解:(1)在AB上取一点G,使AG:GB=AM:MC=FN:NB,
则MG∥BC,NG∥BE,从而平面MNG∥平面CBE,
又MN在平面MNG内,所以 MN∥平面CBE
(2)由(1)知,当AG:GB=AM:MC=FN:NB=2:3时,
平面MGN∥平面CBE.
∴AM:MC=2:3,在线段AB上存在一点G,使平面MGN∥平面CBE,
且AG:GB=2:3.
点评:本题考查直线与平面平行的证明,考查满足条件的点的位置的确定.解题时要认真审题,仔细解答.
(2)由(1)知,当AG:GB=AM:MC=FN:NB=2:3时,平面MGN∥平面CBE.
解答:解:(1)在AB上取一点G,使AG:GB=AM:MC=FN:NB,
则MG∥BC,NG∥BE,从而平面MNG∥平面CBE,
又MN在平面MNG内,所以 MN∥平面CBE
(2)由(1)知,当AG:GB=AM:MC=FN:NB=2:3时,
平面MGN∥平面CBE.
∴AM:MC=2:3,在线段AB上存在一点G,使平面MGN∥平面CBE,
且AG:GB=2:3.
点评:本题考查直线与平面平行的证明,考查满足条件的点的位置的确定.解题时要认真审题,仔细解答.

练习册系列答案
相关题目
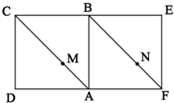 如图,平面内两正方形ABCD与ABEF,点M、N分别在对角线AC、FB上,且AM:MC=FN:NB,沿AB折成直二面角.
如图,平面内两正方形ABCD与ABEF,点M、N分别在对角线AC、FB上,且AM:MC=FN:NB,沿AB折成直二面角.