摘要:(2)设左特征点为.左焦点为.可设直线的方程为
网址:http://m.1010jiajiao.com/timu_id_484817[举报]
设双曲线C:
-
=1的右焦点为F2,过点F2的直线l与双曲线C相交于A,B两点,直线l的斜率为
,且
=2
;
(1)求双曲线C的离心率;
(2)如果F1为双曲线C的左焦点,且F1到l的距离为
,求双曲线C的方程.
查看习题详情和答案>>
| x2 |
| a2 |
| y2 |
| b2 |
| 35 |
| AF2 |
| F2B |
(1)求双曲线C的离心率;
(2)如果F1为双曲线C的左焦点,且F1到l的距离为
2
| ||
| 3 |
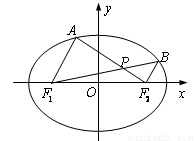
(如图)过椭圆
+
=1(a>b>0)的左焦点F任作一条与两坐标轴都不垂直的弦AB;若点M在x 轴上,且使得MF为△AMB的一条内角平分线,则称点M为该椭圆的“左特征点”.
轴上,且使得MF为△AMB的一条内角平分线,则称点M为该椭圆的“左特征点”.
(1)求椭圆
+y2=1的“左特征点”M的坐标.
(2)试根据(1)中的结论猜测:椭圆
+
=1(a>b>0)的“左特征点”M是一个怎么样的点?并证明你的结论.
查看习题详情和答案>>
| x2 |
| a2 |
| y2 |
| b2 |
 轴上,且使得MF为△AMB的一条内角平分线,则称点M为该椭圆的“左特征点”.
轴上,且使得MF为△AMB的一条内角平分线,则称点M为该椭圆的“左特征点”.(1)求椭圆
| x2 |
| 5 |
(2)试根据(1)中的结论猜测:椭圆
| x2 |
| a2 |
| y2 |
| b2 |
(本题12分)
设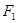 、
、 分别是椭圆
分别是椭圆  的左、右焦点,
的左、右焦点, 是该椭圆上的一个动点,
是该椭圆上的一个动点, 为坐标原点.
为坐标原点.

(1)求 的取值范围;
的取值范围;
(2)设过定点 的直线
的直线 与椭圆交于不同的两点M、N,且∠
与椭圆交于不同的两点M、N,且∠ 为锐角,求直线
为锐角,求直线 的斜率
的斜率 的取值范围.
的取值范围.
查看习题详情和答案>>
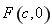

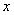


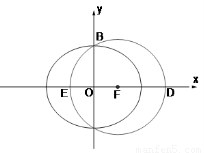
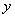
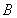
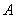



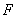
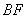
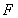

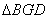
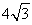
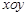 中,椭圆
中,椭圆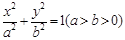 的左、右焦点分别为
的左、右焦点分别为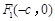 ,
,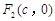 .已知
.已知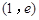 和
和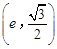 都在椭圆上,其中
都在椭圆上,其中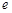 为椭圆的离心率.
为椭圆的离心率.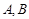 是椭圆上位于
是椭圆上位于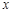 轴上方的两点,且直线
轴上方的两点,且直线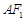 与直线
与直线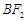 平行,
平行,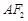 与
与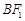 交于点P.
交于点P.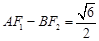 ,求直线
,求直线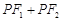 是定值.
是定值.