摘要：直线与圆.圆与圆的位置关系问题 直线与圆的位置关系是本部分考查的一个重要内容.也是高考命题的一个热点.主要涉及轨迹问题.直线与圆位置关系判断.切线方程.弦长.夹角等问题．
网址：http://m.1010jiajiao.com/timu_id_480131[举报]
已知椭圆的中心在原点，焦点在轴上，离心率为
，它与直线
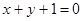相交于P、Q两点，若
，求椭圆方程。
【解析】本试题主要考查了利用椭圆的几何性质以及直线与椭圆的位置关系我们求解椭圆的方程的试题。考查了同学们运用代数的方法来解决几何问题的能力。
查看习题详情和答案>>
已知椭圆的中心在原点，焦点在轴上，离心率为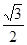
，它与直线
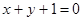相交于P、Q两点，若
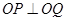，求椭圆方程。
【解析】本试题主要考查了利用椭圆的几何性质以及直线与椭圆的位置关系我们求解椭圆的方程的试题。考查了同学们运用代数的方法来解决几何问题的能力。
查看习题详情和答案>>
（本小题满分12分）. 若直线l：
与抛物线
交于A、B两点，O点是坐标原点。
(1)当m=－1,c=－2时，求证：OA⊥OB；
(2)若OA⊥OB，求证：直线l恒过定点；并求出这个定点坐标。
(3)当OA⊥OB时，试问△OAB的外接圆与抛物线的准线位置关系如何？证明你的结论。
查看习题详情和答案>>
（本小题满分12分）. 若直线l：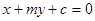
与抛物线
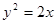交于A、B两点，O点是坐标原点。
(1)当m=－1,c=－2时，求证：OA⊥OB；
(2)若OA⊥OB，求证：直线l恒过定点；并求出这个定点坐标。
(3)当OA⊥OB时，试问△OAB的外接圆与抛物线的准线位置关系如何？证明你的结论。
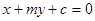与抛物线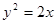交于A、B两点，O点是坐标原点。(1)当m=－1,c=－2时，求证：OA⊥OB；
(2)若OA⊥OB，求证：直线l恒过定点；并求出这个定点坐标。
(3)当OA⊥OB时，试问△OAB的外接圆与抛物线的准线位置关系如何？证明你的结论。
我们知道，直线与圆的位置关系可以用圆心到直线的距离进行判别，那么直线与椭圆的位置关系有类似的判别方法吗？请同学们进行研究并完成下面的问题．
（1）设F1、F2是椭圆M：
+
=1的两个焦点，点F1、F2到直线l：
x-y+
=0的距离分别为d1、d2，试求d1•d2的值，并判断直线l与椭圆M的位置关系．
（2）设F1、F2是椭圆M：
+
=1（a＞b＞0）的两个焦点，点F1、F2到直线l：mx+ny+p=0（m、n不同时为零）的距离分别为d1、d2，且直线l与椭圆M相切，试求d1•d2的值．
（3）试写出一个能判断直线与椭圆的相交、相离位置关系的充要条件（不必证明）．
查看习题详情和答案>>
（1）设F1、F2是椭圆M：
| x2 |
| 25 |
| y2 |
| 9 |
| 2 |
| 5 |
（2）设F1、F2是椭圆M：
| x2 |
| a2 |
| y2 |
| b2 |
（3）试写出一个能判断直线与椭圆的相交、相离位置关系的充要条件（不必证明）．