摘要:可知与轴交于定点.----13分
网址:http://m.1010jiajiao.com/timu_id_478693[举报]
(08年吉林一中文) 椭圆![]() 的两个焦点分别为
的两个焦点分别为![]() ,斜率为
,斜率为![]() 的直线
的直线![]() 过右焦点
过右焦点![]() ,且与椭圆交于
,且与椭圆交于![]() 两点,与
两点,与![]() 轴交于
轴交于![]() 点,点
点,点![]() 分
分![]() 的比为2。
的比为2。
(1).若![]() ,并且弦
,并且弦![]() 的中点到右准线的距离为
的中点到右准线的距离为![]() ,求椭圆的方程。
,求椭圆的方程。
(2).若![]() ,求离心率
,求离心率![]() 的取值范围。
的取值范围。
(本题13分) 已知点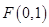 ,直线
,直线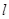 :
: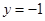 ,
,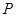 为平面上的动点,过点
为平面上的动点,过点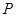 作直线
作直线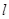 的垂线,垂足为
的垂线,垂足为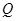 ,且
,且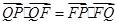 .
.
(1)求动点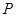 的轨迹
的轨迹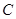 的方程;
的方程;
(2)已知圆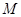 过定点
过定点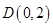 ,圆心
,圆心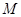 在轨迹
在轨迹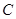 上运动,且圆
上运动,且圆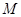 与
与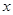 轴交于
轴交于 、
、 两点,设
两点,设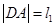 ,
,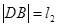 ,求
,求 的最大值.
的最大值.
查看习题详情和答案>>
(本小题满分13分)
已知椭圆![]()
![]() 的离心率为
的离心率为![]() ,以原点为圆心,椭圆的短半轴为半径的圆与直线
,以原点为圆心,椭圆的短半轴为半径的圆与直线![]() 相切.
相切.
(Ⅰ)求椭圆![]() 的方程;
的方程;
(Ⅱ)设![]() ,
,![]() ,
,![]() 是椭圆
是椭圆![]() 上关于
上关于![]() 轴对称的任意两个不同的点,连结
轴对称的任意两个不同的点,连结![]() 交椭圆
交椭圆![]() 于另一点
于另一点![]() ,证明直线
,证明直线![]() 与
与![]() 轴相交于定点
轴相交于定点![]() ;
;
(Ⅲ)在(Ⅱ)的条件下,过点![]() 的直线与椭圆
的直线与椭圆![]() 交于
交于![]() ,
,![]() 两点,求
两点,求![]() 的取值范围.
的取值范围.