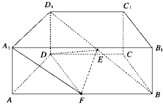
摘要：18．直四棱柱ABCD―A1B1C1D1中.底面ABCD为直角梯形.∠BAD=∠ABC=900.AB=BC=1.AD=AA1=2.E为侧棱BB1的中点.(1)求证:EC1∥AD1,(2)在线段AD上求一点F.使EF⊥平面ACD1;(3)求平面EAC1与底面ABCD所成的锐二面角的大小. 解答(1)以A为原点.AB.AD.AA1分别为x.y.z轴建立空间直角坐标系
网址：http://m.1010jiajiao.com/timu_id_478674[举报]
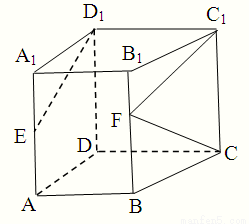
在直四棱柱ABCD-A1B1C1D1中，底面ABCD为直角梯形，∠BAD=∠ADC=90°，AB=AD=1，CD=CC1=2，E为棱AA1的中点，F为棱BB1上的动点．（Ⅰ）试确定点F的位置，使得D1E⊥DF；
（Ⅱ）在（Ⅰ）的条件下，求CF与平面EFD1所成角的大小．
在直四棱柱ABCD-A1B1C1D1中，底面ABCD为直角梯形，∠BAD=∠ADC=90°，AB=AD=1，CD=CC1=2，E为棱AA1的中点，F为棱BB1上的动点．
（Ⅰ）试确定点F的位置，使得D1E⊥DF；
（Ⅱ）在（Ⅰ）的条件下，求CF与平面EFD1所成角的大小．
查看习题详情和答案>>
在直四棱柱ABCD-A1B1C1D1中，底面ABCD为直角梯形，∠BAD=∠ADC=90°，AB=AD=1，CD=CC1=2，E为棱AA1的中点，F为棱BB1上的动点．
（Ⅰ）试确定点F的位置，使得D1E⊥DF；
（Ⅱ）在（Ⅰ）的条件下，求CF与平面EFD1所成角的大小．
查看习题详情和答案>>
（Ⅰ）试确定点F的位置，使得D1E⊥DF；
（Ⅱ）在（Ⅰ）的条件下，求CF与平面EFD1所成角的大小．
查看习题详情和答案>>
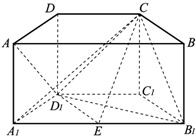如图，直四棱柱ABCD-A1B1C1D1中，底面ABCD为梯形，AB平行于CD，