摘要：∴二面角C-PA-B的大小为arccos．------------14分5(和平区2008年高考数学. 如图.直二面角D―AB―E中.四边形ABCD是边长为2的正方形.AE=EB.F为CE上的点.且BF⊥平面ACE.(1)求证:AE⊥平面BCE,(2)求二面角B―AC―E的大小,(3)求点D到平面ACE的距离.
网址：http://m.1010jiajiao.com/timu_id_476501[举报]
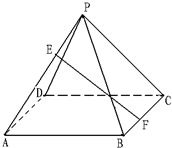如图，正四棱锥中P-ABCD，点E，F分别在棱PA，BC上，且AE=2PE，（1）问点F在何处时，EF⊥AD？
（2）当EF⊥AD且正三角形PAB的边长为a时，求点F到平面PAB的距离；
（3）在第（2）条件下，求二面角C-PA-B的大小． 查看习题详情和答案>>
如图，正四棱锥中P-ABCD，点E，F分别在棱PA，BC上，且AE=2PE，
（1）问点F在何处时，EF⊥AD？
（2）当EF⊥AD且正三角形PAB的边长为a时，求点F到平面PAB的距离；
（3）在第（2）条件下，求二面角C-PA-B的大小．
查看习题详情和答案>>
（1）问点F在何处时，EF⊥AD？
（2）当EF⊥AD且正三角形PAB的边长为a时，求点F到平面PAB的距离；
（3）在第（2）条件下，求二面角C-PA-B的大小．
查看习题详情和答案>>
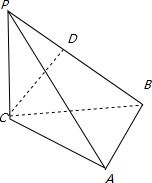如图，三棱锥P-ABC中，PC⊥平面ABC，PC=AC=2，AB=BC，D是PB上一点，且CD⊥平面PAB．（1）求证：AB⊥平面PCB；
（2）求二面角C-PA-B的大小的余弦值． 查看习题详情和答案>>
（2007•东城区一模）如图，三棱锥P-ABC中，PC⊥平面ABC，PC=AC=2，AB=BC，D是PB上一点，且CD⊥平面PAB．
（2008•宣武区一模）如图，三棱锥P-ABC中，PC⊥平面ABC，PC=AC=2，AB=BC，D是PB上一点，且CD⊥平面PAB