摘要:答案:(1)取AC的中点H.连MH.则MH//PA.所以MH⊥平面ABCD.过H作HN⊥AD于N.连MN.由三垂线定理可得MN⊥AD.则∠MNH就为所求的二面角的平面角.------2分
网址:http://m.1010jiajiao.com/timu_id_476277[举报]
如图,在正三棱柱ABC-A1B1C1中,E∈BB1,截面A1EC⊥侧面AC1.
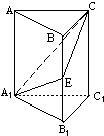
(1)求证:BE=EB1;
(2)若AA1=A1B1;求平面A1EC与平面A1B1C1所成二面角(锐角)的度数.
注意:在下面横线上填写适当内容,使之成为(Ⅰ)的完整证明,并解答(Ⅱ).
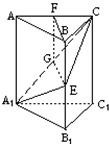
(1)证明:在截面A1EC内,过E作EG⊥A1C,G是垂足.
①∵
∴EG⊥侧面AC1;取AC的中点F,连接BF,FG,由AB=BC得BF⊥AC,
②∵
∴BF⊥侧面AC1;得BF∥EG,BF、EG确定一个平面,交侧面AC1于FG.
③∵
∴BE∥FG,四边形BEGF是平行四边形,BE=FG,
④∵
∴FG∥AA1,△AA1C∽△FGC,
⑤∵
∴FG=
AA1=
BB1,即BE=
BB1,故BE=EB1.
查看习题详情和答案>>

(1)求证:BE=EB1;
(2)若AA1=A1B1;求平面A1EC与平面A1B1C1所成二面角(锐角)的度数.
注意:在下面横线上填写适当内容,使之成为(Ⅰ)的完整证明,并解答(Ⅱ).

(1)证明:在截面A1EC内,过E作EG⊥A1C,G是垂足.
①∵
∴EG⊥侧面AC1;取AC的中点F,连接BF,FG,由AB=BC得BF⊥AC,
②∵
∴BF⊥侧面AC1;得BF∥EG,BF、EG确定一个平面,交侧面AC1于FG.
③∵
∴BE∥FG,四边形BEGF是平行四边形,BE=FG,
④∵
∴FG∥AA1,△AA1C∽△FGC,
⑤∵
∴FG=
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
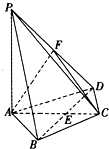 如图所示,已知PA⊥平面ABCD,PA=AB=AD=2,AC与BD交于E点,BD=2,BC=CD=
如图所示,已知PA⊥平面ABCD,PA=AB=AD=2,AC与BD交于E点,BD=2,BC=CD=| 2 |
(1)取PD的中点F,求证:PB∥平面AFC;
(2)求多面体PABCF的体积.
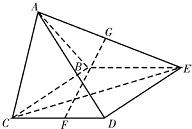 如图,在四棱锥A-BCDE中,底面BCDE为矩形,AB=AC,BC=2,CD=1,并且侧面ABC⊥底面BCDE.
如图,在四棱锥A-BCDE中,底面BCDE为矩形,AB=AC,BC=2,CD=1,并且侧面ABC⊥底面BCDE.(1)取CD的中点为F,AE的中点为G,证明:FG∥面ABC;
(2)试在线段BC上确定点M,使得AE⊥DM,并加以证明. 查看习题详情和答案>>
(12分)
学校欲在操场边上一直角三角形空地ABC上种植草坪,并需铺设一根水管EF(E在AC上,F在AB上)用于灌溉,已知∠A=30°,∠C=90°,BC=2a,D是BC中点,为确保灌溉的效果,铺设时要求∠EDF=60°。现有两种方案可供参考。甲方案:取AC的中点E铺设水管;乙方案:取AB的中点F铺设水管。

(1)比较甲乙两种方案,哪一种方案更合理(EF的长较小的合理);
(2)学校研究小组通过研究得出:无论D在BC的什么位置,总存在E,F两点,使△DEF为正三角形。试证明该结论的正确性。
查看习题详情和答案>>
如图,在正三棱柱ABC-A1B1C1中,E∈BB1,截面A1EC⊥侧面AC1.
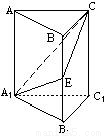
(1)求证:BE=EB1;
(2)若AA1=A1B1;求平面A1EC与平面A1B1C1所成二面角(锐角)的度数.
注意:在下面横线上填写适当内容,使之成为(Ⅰ)的完整证明,并解答(Ⅱ).
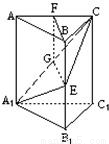
(1)证明:在截面A1EC内,过E作EG⊥A1C,G是垂足.
①∵______
∴EG⊥侧面AC1;取AC的中点F,连接BF,FG,由AB=BC得BF⊥AC,
②∵______
∴BF⊥侧面AC1;得BF∥EG,BF、EG确定一个平面,交侧面AC1于FG.
③∵______
∴BE∥FG,四边形BEGF是平行四边形,BE=FG,
④∵______
∴FG∥AA1,△AA1C∽△FGC,
⑤∵______
∴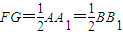 ,即
,即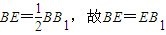 .
.
查看习题详情和答案>>

(1)求证:BE=EB1;
(2)若AA1=A1B1;求平面A1EC与平面A1B1C1所成二面角(锐角)的度数.
注意:在下面横线上填写适当内容,使之成为(Ⅰ)的完整证明,并解答(Ⅱ).

(1)证明:在截面A1EC内,过E作EG⊥A1C,G是垂足.
①∵______
∴EG⊥侧面AC1;取AC的中点F,连接BF,FG,由AB=BC得BF⊥AC,
②∵______
∴BF⊥侧面AC1;得BF∥EG,BF、EG确定一个平面,交侧面AC1于FG.
③∵______
∴BE∥FG,四边形BEGF是平行四边形,BE=FG,
④∵______
∴FG∥AA1,△AA1C∽△FGC,
⑤∵______
∴
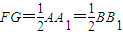 ,即
,即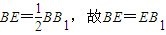 .
.查看习题详情和答案>>