摘要：如图.在四棱锥P―ABCD中.PA⊥平面ABCD.四边形ABCD为直角梯形.AD//BC且AD>BC.∠DAB=∠ABC=90°.PA=.AB=BC=1.M为PC的中点.(1)求二面角M―AD―C的大小,(2)如果∠AMD=90°.求线段AD的长.
网址：http://m.1010jiajiao.com/timu_id_476276[举报]
如图，在四棱锥P-ABCD中，PA⊥平面ABCD，底面ABCD是直线梯形，∠ADC为直角，AD∥BC，AB⊥AC，AC=AB=2，G是△PAC的重心，E为PB中点，F在线段BC上，且CF=2FB．（1）证明：FG∥平面PAB；
（2）证明：FG⊥AC；
（3）求二面角P-CD-A的一个三角函数值，使得FG⊥平面AEC 查看习题详情和答案>>
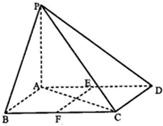如图，在四棱锥P-ABCD中，PA⊥平面ABCD，底面ABCD为平行四边形，且AB=1，BC=2，∠ABC=| π | 3 |
（I）求证：EF∥面PCD；
（II）求证：AC⊥平面PAB． 查看习题详情和答案>>
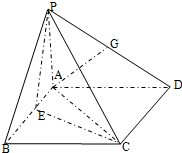如图，在四棱锥P-ABCD中，PA⊥平面ABCD，四边形ABCD为正方形，PA=AB=4，G为PD中点，E点在AB上，平面PEC⊥平面PDC．（Ⅰ）求证：AG⊥平面PCD；
（Ⅱ）求证：AG∥平面PEC；
（Ⅲ）求点G到平面PEC的距离． 查看习题详情和答案>>
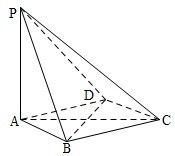如图，在四棱锥P-ABCD中，PA⊥平面ABCD，底面ABCD是菱形，AB=2，∠BAD=60°．
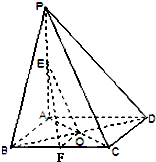如图，在四棱锥P-ABCD中，PA⊥平面ABCD，E为PA的中点，F为BC的中点，底面ABCD是菱形，对角线AC，BD交于点O．求证：