摘要:(2) 在线段BC上取点P,使BP=BC=,过P作PQ⊥CD于点Q, ∴ PQ⊥平面ACD
网址:http://m.1010jiajiao.com/timu_id_476246[举报]
 (2012•枣庄二模)已知在四棱锥P-ABCD中,底面ABCD是矩形,且AD=2,AB=1,PA⊥平面ABCD,E、F分别是线段AB、BC的中点.
(2012•枣庄二模)已知在四棱锥P-ABCD中,底面ABCD是矩形,且AD=2,AB=1,PA⊥平面ABCD,E、F分别是线段AB、BC的中点.(1)证明:DF⊥平面PAF;
(2)在线段AP上取点G使AG=
| 1 | 4 |
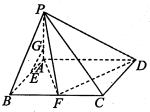 已知在四棱锥P-ABCD中,底面ABCD是矩形,且AD=2,AB=1,PA⊥平面ABCD,E、F分别是线段AB、BC的中点.
已知在四棱锥P-ABCD中,底面ABCD是矩形,且AD=2,AB=1,PA⊥平面ABCD,E、F分别是线段AB、BC的中点.
(1)证明:DF⊥平面PAF;
(2)在线段AP上取点G使AG= AP,求证:EG∥平面PFD.
AP,求证:EG∥平面PFD.
查看习题详情和答案>>
已知在四棱锥P-ABCD中,底面ABCD是矩形,且AD=2,AB=1,PA⊥平面ABCD,E、F分别是线段AB、BC的中点.
(1)证明:DF⊥平面PAF;
(2)在线段AP上取点G使AG= AP,求证:EG∥平面PFD.
AP,求证:EG∥平面PFD.
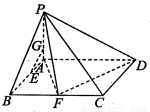 查看习题详情和答案>>
查看习题详情和答案>>
(1)证明:DF⊥平面PAF;
(2)在线段AP上取点G使AG=
 AP,求证:EG∥平面PFD.
AP,求证:EG∥平面PFD. 查看习题详情和答案>>
查看习题详情和答案>>
