题目内容

已知椭圆C:x2+2y2=8和点P(4,1),过P作直线交椭圆于A、B两点,在线段AB上取点Q,使=λ,=-λ,求动点Q的轨迹所在曲线的方程及点Q的横坐标的取值范围.

解:设A(x1,y1),B(x2,y2),Q(x,y),则由=λ,=-λ,

可得=,解之,得x=.①       

设直线AB的方程为y=k(x-4)+1,代入椭圆C的方程,消去y得出关于x的一元二次方程

(2k2+1)x2+4k(1-4k)x+2(1-4k)2-8=0.②

∴

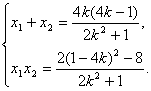
代入①,化简得x=.③       

与y=k(x-4)+1联立,消去k得(2x+y-4)(x-4)=0.

在②中,由Δ=-64k2+64k+24＞0,

解得＜k＜.

结合③可求得＜x＜.

故知点Q的轨迹方程为2x+y-4=0(＜x＜).

练习册系列答案
相关题目
已知椭圆C的对称中心为坐标原点O，焦点在x轴上，左右焦点分别为F1，F2，且|F1F2|=2
5
，点(
5
，
4
3
)在该椭圆上．
（1）求椭圆C的方程；
（2）设椭圆C上的一点p在第一象限，且满足PF1⊥PF2，⊙O的方程为x2+y2=4．求点p坐标，并判断直线pF2与⊙O的位置关系；
（3）设点A为椭圆的左顶点，是否存在不同于点A的定点B，对于⊙O上任意一点M，都有
MB
MA
为常数，若存在，求所有满足条件的点B的坐标；若不存在，说明理由．
已知椭圆C：
x2
a2
+
y2
b2
=1（a＞b＞0）的两个焦点和短轴的两个端点都在圆x2+y2=1上．
（I）求椭圆C的方程；
（Ⅱ）若斜率为k的直线过点M（2，0），且与椭圆C相交于A，B两点．试探讨k为何值时，三角形OAB为直角三角形．
已知椭圆C：
x2
a2
+
y2
b2
=1（a＞b＞0）的左右焦点F1、F2与短轴一端点的连线互相垂直，M为椭圆上任一点，且△MF1F2的面积最大值为1．
（1）求椭圆C的方程；
（2）设圆A：x2+y2=
2
3
的切线l与椭圆C交于P、Q两点，求以坐标原点O及P、Q三点为顶点的△OPQ的外接圆面积的最大值．
如图所示，已知椭圆C的离心率为
3
2
，A、B、F分别为椭圆的右顶点、上顶点、右焦点，且S△ABF=1-
3
2
．
（1）求椭圆C的方程；
（2）已知直线l：y=kx+m被圆O：x2+y2=4所截弦长为2
3
，若直线l与椭圆C交于M、N两点．求△OMN面积的最大值．
已知椭圆C：
x2
a2
+
y2
b2
=1（a＞b＞0）的离心率为
5
3
，短轴一个端点到右焦点的距离为3．
（1）求椭圆C的方程；
（2）椭圆C上是否存在点P，使得过点P引圆O：x2+y2=b2的两条切线PA、PB互相垂直？若存在，请求出点P的坐标；若不存在，请说明理由．

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网