请阅读并回答问题：
在解分式方程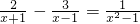时，小跃的解法如下：
解：方程两边同乘以（x+1）（x-1），得2（x-1）-3=1．①2x-1-3=1．②
解得　　　　　　．
检验：时，（x+1）（x-1）≠0，③
所以是原分式方程的解．④
（1）你认为小跃在哪里出现了错误______（只填序号）；
（2）针对小跃解分式方程时出现的错误和解分式方程中的其它重要步骤，请你提出至少三个改进的建议．

用配方法解下列方程：
（1）x²+4x-5=0，解：移项，得x²+4x=______，方程两边同时加上4，得x²+4x+4=______，
即（x+2）²=______，所以x+2=______或x+2=______，所以x₁=______，x₂=______．
（2）2y²-5y+2=0，解：方程两边同除以2，得y²-y=______，
方程两边同加上（）²，得y²-y+（）²=______，
所以（______）²=______，解得y₁=______，y₂=______．

下列变形中：
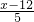①由方程=2去分母，得x-12=10；
②由方程x=两边同除以，得x=1；
③由方程6x-4=x+4移项，得7x=0；
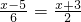④由方程2-两边同乘以6，得12-x-5=3（x+3）．
错误变形的个数是_____个．

1. A.
   4
2. B.
   3
3. C.
   2
4. D.
   1