题目内容
请阅读并回答问题:
在解分式方程
-
=
时,小跃的解法如下:
解:方程两边同乘以(x+1)(x-1),得2(x-1)-3=1.①2x-1-3=1.②
解得 x=
.
检验:x=
时,(x+1)(x-1)≠0,③
所以x=
是原分式方程的解.④
(1)你认为小跃在哪里出现了错误
(2)针对小跃解分式方程时出现的错误和解分式方程中的其它重要步骤,请你提出至少三个改进的建议.
在解分式方程
| 2 |
| x+1 |
| 3 |
| x-1 |
| 1 |
| x2-1 |
解:方程两边同乘以(x+1)(x-1),得2(x-1)-3=1.①2x-1-3=1.②
解得 x=
| 5 |
| 2 |
检验:x=
| 5 |
| 2 |
所以x=
| 5 |
| 2 |
(1)你认为小跃在哪里出现了错误
①②
①②
(只填序号);(2)针对小跃解分式方程时出现的错误和解分式方程中的其它重要步骤,请你提出至少三个改进的建议.
分析:(1)出现错误的序号为①②,原因是去分母与去括号出现错误;
(2)去分母时注意等号两边各项都乘以最简公分母,去括号时注意正确使用去括号法则,解方程求出x的值要进行检验.
(2)去分母时注意等号两边各项都乘以最简公分母,去括号时注意正确使用去括号法则,解方程求出x的值要进行检验.
解答:解:(1)①②;
(2)去分母时注意等号两边各项都乘以最简公分母,去括号时注意正确使用去括号法则,解方程求出x的值要进行检验.
正确解法为:去分母得:2(x-1)-3(x+1)=1,
去括号得:2x-2-3x-3=1,
解得:x=-6,
经检验x=-6是分式方程的解.
故答案为:①②
(2)去分母时注意等号两边各项都乘以最简公分母,去括号时注意正确使用去括号法则,解方程求出x的值要进行检验.
正确解法为:去分母得:2(x-1)-3(x+1)=1,
去括号得:2x-2-3x-3=1,
解得:x=-6,
经检验x=-6是分式方程的解.
故答案为:①②
点评:此题考查了解分式方程,解分式方程的基本思想是“转化思想”,把分式方程转化为整式方程求解.解分式方程一定注意要验根.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目

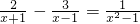 时,小跃的解法如下:
时,小跃的解法如下: .
.