摘要：解:.．经检验..是原方程的根
网址：http://m.1010jiajiao.com/timu_id_475036[举报]
解方程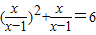
的步骤如下：
①设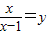
，则原方程化为y2+y=6，解这个方程，得y1=-3，y2=2
②当y1=-3时，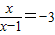
，∴x=-3x+3，∴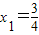
③当y2=2时，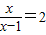
，∴x=2x-2，∴x2=2
④经检验，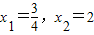
都是原方程的根
以上各步骤中，所有的正确的步骤是（ ）
A．①
B．①②
C．①②③
D．①②③④
查看习题详情和答案>>
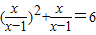的步骤如下：①设
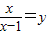，则原方程化为y2+y=6，解这个方程，得y1=-3，y2=2②当y1=-3时，
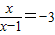，∴x=-3x+3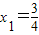，∴③当y2=2时，
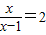，∴x=2x-2，∴x2=2④经检验，
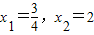都是原方程的根以上各步骤中，所有的正确的步骤是（ ）
A．①
B．①②
C．①②③
D．①②③④
查看习题详情和答案>>
小玲解方程：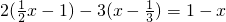
的步骤如下：
（1）去括号，得x-2-3x-1=1-x；
（2）移项，得-2x+x=1+3；
（3）合并同类项，得-x=4；
（4）最后得x=-4．
但是经过检验知道，x=-4不是原方程的根．请你检查一下，上述解题过程哪里错了？并予以改正．
查看习题详情和答案>>
用“拆项法”解分式方程
大家知道，解分式方程的基本方法是，把方程的两边同乘以各分母的最简公分母，化为整式方程来解，而对于一些特殊的分式方程来说，采用上述方法往往越解越繁．下面我们介绍一种简捷、明快的方法－－拆项法．
例：解方程
解：先降低方程中各分式分子的次数，将原方程变形为
即(4＋
)－(7＋
)＝(1－
)－(4－
)
整理得
两边各自通分得
∴(x－2)(x－1)＝(x－7)(x－6)
即x2－3x＋2＝x2－13x＋42
也即10x＝40 ∴x＝4
经检验知，x＝4是原方程的根．
请你运用上述方法，解分式方程
