摘要：解:(1) ．
网址：http://m.1010jiajiao.com/timu_id_474687[举报]
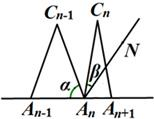
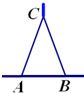小知识：如图，我们称两臂长度相等（即CA=CB）的圆规为等臂圆规．当等臂圆规的两脚摆放在一条直线上时，若张角∠ACB=x°，则底角∠CAB=∠CBA=（90-| x | 2 |
请运用上述知识解决问题：如图，n个相同规格的等臂圆规的两脚依次摆放在同一条直线上，其张角度数变化如下：∠A1C1A2=160°，∠A2C2A3=80°，∠A3C3A4=40°，∠A4C4A5=20°，…
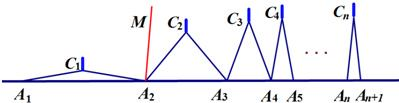
（1）①由题意可得∠A1A2C1=
②若A2M平分∠A3A2C1，则∠MA2C2=
（2）∠An+1AnCn=
（3）当n≥3时，设∠An-1AnCn-1的度数为a，∠An+1AnCn-1的角平分线AnN与AnCn构成的角的度数为β，那么a与β之间的等量关系是
小明、小华、小颖三名同学解这样一个问题：
求a为何值时，
=
成立．
小明：因为a2+2a-3=（a-1）（a+3），从分式的右边知，分式的分子和分母同时除以a-1，只需a-1≠0即可，故a的取值范围是a≠1；
小华：因为a+3也不能为零，故还应加上a≠-3这个条件，即a的取值范围就是a≠-3且a≠1；
小颖：因为|a-1|=±（a-1），要使分子、分母约去a-1，则必须满足a-1≥0，结合a≠1和a≠-3解出a＞1，即a的取值范围为a＞1．
三名同学中谁说的有道理呢（ ）
求a为何值时，
| |a-1| |
| a2+2a-3 |
| 1 |
| a+3 |
小明：因为a2+2a-3=（a-1）（a+3），从分式的右边知，分式的分子和分母同时除以a-1，只需a-1≠0即可，故a的取值范围是a≠1；
小华：因为a+3也不能为零，故还应加上a≠-3这个条件，即a的取值范围就是a≠-3且a≠1；
小颖：因为|a-1|=±（a-1），要使分子、分母约去a-1，则必须满足a-1≥0，结合a≠1和a≠-3解出a＞1，即a的取值范围为a＞1．
三名同学中谁说的有道理呢（ ）
| A、小明 | B、小华 |
| C、小颖 | D、都有道理 |
24、小明家使用的是分时电表，按平时段（6：00-22：00）和谷时段（22：00一次日6：00）分别计费，平时段每度电价为0.61元，谷时段每度电价为0.30元，小明将家里2005年1月至5月的平时段和谷时段的用电量分别用折线图表示（如图），同时将前4个月的用电量和相应电费制成表格（如表）| 月用电量（度） | 电费（元） | |
| 1月 | 90 | 51.80 |
| 2月 | 92 | 50.85 |
| 3月 | 98 | 49.24 |
| 4月 | 105 | 48.55 |
| 5月 |
（1）计算5月份的用电量和相应电费，将所得结果填入表1中；
（2）小明家这5个月的月平均用电量为度；
（3）小明家这5个月的月平均用电量呈趋势（选择“上升”或“下降”）；这5个月每月电费呈趋势（选择“上升”或“下降”）；
（4）小明预计7月份家中用电量很大，估计7月份用电量可达500度，相应电费将达243元，请你根据小明的估计，计算出7月份小明家平时段用电量和谷时段用电量．
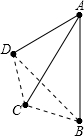
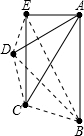
小明在阅览时发现这样一个问题“在某次聚会中，共有6人参加，如果每两人都握一次手，共握几次手？”，小明通过努力得出了答案．为了解决更一般的问题，小明设计了下列图表进行探究：请你在图表右下角的横线上填上你归纳出的一般结论．
查看习题详情和答案>>
| 参加人数 | 2 | 3 | 4 | 5 | … | n |
| 握手示意图 |  |
 |
 |
 |
 | |
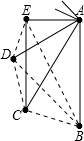| 握手次数 | 1 | 2+1=3 | 3+2+1=6 | 4+3+2+1=10 | … |