摘要:解:(1)由.令.得...
网址:http://m.1010jiajiao.com/timu_id_474666[举报]
首先,我们看两个问题的解答:
问题1:已知x>0,求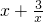 的最小值.
的最小值.
问题2:已知t>2,求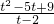 的最小值.
的最小值.
问题1解答:对于x>0,我们有: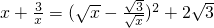 ≥
≥ .当
.当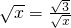 ,即
,即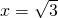 时,上述不等式取等号,所以
时,上述不等式取等号,所以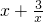 的最小值
的最小值 .
.
问题2解答:令x=t-2,则t=x+2,于是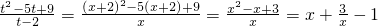 .
.
由问题1的解答知,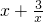 的最小值
的最小值 ,所以
,所以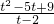 的最小值是
的最小值是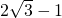 .
.
弄清上述问题及解答方法之后,解答下述问题:
在直角坐标系xOy中,一次函数y=kx+b(k>0,b>0)的图象与x轴、y轴分别交于A、B两点,且使得△OAB的面积值等于|OA|+|OB|+3.
(1)用b表示k;
(2)求△AOB面积的最小值.
查看习题详情和答案>>
首先,我们看两个问题的解答:
问题1:已知x>0,求 的最小值.
的最小值.
问题2:已知t>2,求 的最小值.
的最小值.
问题1解答:对于x>0,我们有: ≥
≥ .当
.当 ,即
,即 时,上述不等式取等号,所以
时,上述不等式取等号,所以 的最小值
的最小值 .
.
问题2解答:令x=t-2,则t=x+2,于是 .
.
由问题1的解答知, 的最小值
的最小值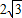 ,所以
,所以 的最小值是
的最小值是 .
.
弄清上述问题及解答方法之后,解答下述问题:
在直角坐标系xOy中,一次函数y=kx+b(k>0,b>0)的图象与x轴、y轴分别交于A、B两点,且使得△OAB的面积值等于|OA|+|OB|+3.
(1)用b表示k;
(2)求△AOB面积的最小值.
查看习题详情和答案>>
问题1:已知x>0,求
 的最小值.
的最小值.问题2:已知t>2,求
 的最小值.
的最小值.问题1解答:对于x>0,我们有:
 ≥
≥ .当
.当 ,即
,即 时,上述不等式取等号,所以
时,上述不等式取等号,所以 的最小值
的最小值 .
.问题2解答:令x=t-2,则t=x+2,于是
 .
.由问题1的解答知,
 的最小值
的最小值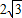 ,所以
,所以 的最小值是
的最小值是 .
.弄清上述问题及解答方法之后,解答下述问题:
在直角坐标系xOy中,一次函数y=kx+b(k>0,b>0)的图象与x轴、y轴分别交于A、B两点,且使得△OAB的面积值等于|OA|+|OB|+3.
(1)用b表示k;
(2)求△AOB面积的最小值.
查看习题详情和答案>>
如图半径分别为m,n(0<m<n)的两圆⊙O1和⊙O2相交于P,Q两点,且点P(4,1),两圆同时与两坐标轴相切,⊙O1与x轴,y轴分别切于点M,点N,⊙O2与x轴,y轴分别切于点R,点H.
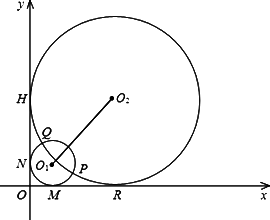
(1)求两圆的圆心O1,O2所在直线的解析式;
(2)求两圆的圆心O1,O2之间的距离d;
(3)令四边形PO1QO2的面积为S1,四边形RMO1O2的面积为S2.
试探究:是否存在一条经过P,Q两点、开口向下,且在x轴上截得的线段长为![]() 的抛物线?若存在,亲、请求出此抛物线的解析式;若不存在,请说明理由.
的抛物线?若存在,亲、请求出此抛物线的解析式;若不存在,请说明理由.
阅读理解:将下列二次三项式在实数范围内分解因式:
(1)x2-5x+6;(2)x2-2x+1;(3)4x2+8x-1.
解:(1)令x2-5x+6=0,解得方程的两根为x1=2,x2=3.则x2-5x+6=(x-2)(x-3)
(2)令x2-2x+1=0,解得方程的两根为x1=x2=1,则x2-2x+1=(x-1)2;
(3)令4x2+8x-1=0,解得方程的两根为x1=
,x2=
,则4x2+8x-1=4(x-
)(x-
)=(2x+2-
)(2x+2+
)
参考以上解答下列问题:
在实数范围内因式分解:
①25x2+10x+1②4x2-8x+1
二次三项式2x2-3x+2在实数范围内能分解因式吗?如果能,请你分解出来;如果不能分解,请说明理由. 查看习题详情和答案>>
(1)x2-5x+6;(2)x2-2x+1;(3)4x2+8x-1.
解:(1)令x2-5x+6=0,解得方程的两根为x1=2,x2=3.则x2-5x+6=(x-2)(x-3)
(2)令x2-2x+1=0,解得方程的两根为x1=x2=1,则x2-2x+1=(x-1)2;
(3)令4x2+8x-1=0,解得方程的两根为x1=
-2+
| ||
| 2 |
-2-
| ||
| 2 |
-2-
| ||
| 2 |
-2-
| ||
| 2 |
| 5 |
| 5 |
参考以上解答下列问题:
在实数范围内因式分解:
①25x2+10x+1②4x2-8x+1
二次三项式2x2-3x+2在实数范围内能分解因式吗?如果能,请你分解出来;如果不能分解,请说明理由. 查看习题详情和答案>>
 ,则4x2+8x-1=4(x-
,则4x2+8x-1=4(x- )(
)(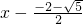 )=(
)=( )(
)( )
)