题目内容
阅读理解:将下列二次三项式在实数范围内分解因式:(1)x2-5x+6;(2)x2-2x+1;(3)4x2+8x-1.
解:(1)令x2-5x+6=0,解得方程的两根为x1=2,x2=3.则x2-5x+6=(x-2)(x-3)
(2)令x2-2x+1=0,解得方程的两根为x1=x2=1,则x2-2x+1=(x-1)2;
(3)令4x2+8x-1=0,解得方程的两根为x1=
-2+
| ||
| 2 |
-2-
| ||
| 2 |
-2-
| ||
| 2 |
-2-
| ||
| 2 |
| 5 |
| 5 |
参考以上解答下列问题:
在实数范围内因式分解:
①25x2+10x+1②4x2-8x+1
二次三项式2x2-3x+2在实数范围内能分解因式吗?如果能,请你分解出来;如果不能分解,请说明理由.
分析:根据范例的解答过程,先分别令各个二次三项式等于0,得到关于x的一元二次方程,再解出各一元二次方程的解,根据公式ax2+bx+c=a(x-x1)(x-x2)分解即可.
解答:解:①令25x2+10x+1=0,解得方程的两根为x1=x2=-
.则25x2+10x+1=25(x+
)2;
②令4x2-8x+1=0,解得方程的两根为x1=
,x2=
.
则4x2-8x+1=4(x-
)(x-
);
③令2x2-3x+2=0,由于△=b2-4ac=(-3)2-4×2×2=-7<0,所以方程无实根,
所以二次三项式2x2-3x+2在实数范围内不能分解因式.
| 1 |
| 5 |
| 1 |
| 5 |
②令4x2-8x+1=0,解得方程的两根为x1=
2+
| ||
| 2 |
2-
| ||
| 2 |
则4x2-8x+1=4(x-
2+
| ||
| 2 |
2-
| ||
| 2 |
③令2x2-3x+2=0,由于△=b2-4ac=(-3)2-4×2×2=-7<0,所以方程无实根,
所以二次三项式2x2-3x+2在实数范围内不能分解因式.
点评:本题考查十字相乘法分解因式,在实数范围内分解因式的步骤是:首先令二次三项式等于0,然后解一元二次方程,方程有解,则根据ax2+bx+c=a(x-x1)(x-x2)公式分解,若方程无解,则原二次三项式不能分解因式.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
 ,则4x2+8x-1=4(x-
,则4x2+8x-1=4(x- )(
)(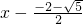 )=(
)=( )(
)( )
) ,则4x2+8x-1=4(x-
,则4x2+8x-1=4(x- )(
)( )=(
)=( )(
)( )
)