摘要:∵OP==4∴△POA是等边三角形图1
网址:http://m.1010jiajiao.com/timu_id_474593[举报]
 如图,P是反比例函数y=
如图,P是反比例函数y=| k | x |
(1)当点P的横坐标逐渐增大时,△POA的面积将如何变化?
(2)若△POA为等边三角形,求此反比例函数的解析式.
在平面直角坐标系中,M是双曲线y=-
(x<0)上一点,把双曲线y=-
(x<0)关于y轴作对称,点M的对称点为N,N点坐标为(m,6),作NA⊥x轴于A,NB⊥y轴于B.
(1)如图1,以OA为一边在四边形OANB内部作等边△OAC,求点C的坐标;
(2)在(1)的前提下,在平面内找到点D,使以O、C、N、D为顶点的四边形为平行四边形,直接写出点D的坐标;
(3)如图2,若在四边形BOAN内部有一点P,满足∠PBN=∠PNB=15°,连接PO、PA.求证:△POA为等边三角形.

查看习题详情和答案>>
| 36 |
| x |
| 36 |
| x |
(1)如图1,以OA为一边在四边形OANB内部作等边△OAC,求点C的坐标;
(2)在(1)的前提下,在平面内找到点D,使以O、C、N、D为顶点的四边形为平行四边形,直接写出点D的坐标;
(3)如图2,若在四边形BOAN内部有一点P,满足∠PBN=∠PNB=15°,连接PO、PA.求证:△POA为等边三角形.

感受理解
如图①,△ABC是等边三角形,AD、CE分别是∠BAC、∠BCA的平分线,AD、CE相交于点F,则线段FE与FD之间的数量关系是
自主学习
事实上,在解决几何线段相等问题中,当条件中遇到角平分线时,经常采用下面构造全等三角形的解决思路
如:在图②中,若C是∠MON的平分线OP上一点,点A在OM上,此时,在ON上截取OB=OA,连接BC,根据三角形全等判定(SAS),容易构造出全等三角形△OBC和△OAC,从而得到线段CA与CB相等
学以致用
参考上述学到的知识,解答下列问题:
如图③,△ABC不是等边三角形,但∠B=60°,AD、CE分别是∠BAC、∠BCA的平分线,AD、CE相交于点F.求证:FE=FD.
查看习题详情和答案>>
如图①,△ABC是等边三角形,AD、CE分别是∠BAC、∠BCA的平分线,AD、CE相交于点F,则线段FE与FD之间的数量关系是
EF=FD
EF=FD
自主学习
事实上,在解决几何线段相等问题中,当条件中遇到角平分线时,经常采用下面构造全等三角形的解决思路
如:在图②中,若C是∠MON的平分线OP上一点,点A在OM上,此时,在ON上截取OB=OA,连接BC,根据三角形全等判定(SAS),容易构造出全等三角形△OBC和△OAC,从而得到线段CA与CB相等
学以致用
参考上述学到的知识,解答下列问题:
如图③,△ABC不是等边三角形,但∠B=60°,AD、CE分别是∠BAC、∠BCA的平分线,AD、CE相交于点F.求证:FE=FD.

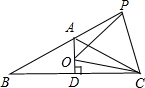 已知如图等腰△ABC,AB=AC,∠BAC=120°,AD⊥BC于点D,点P是BA延长线上一点,点O是线段AD上一点,OP=OC,下面的结论:①∠APO+∠DCO=30°;②△OPC是等边三角形;③AC=AO+AP;④S△ABC=S四边形AOCP.其中正确的有( )个.
已知如图等腰△ABC,AB=AC,∠BAC=120°,AD⊥BC于点D,点P是BA延长线上一点,点O是线段AD上一点,OP=OC,下面的结论:①∠APO+∠DCO=30°;②△OPC是等边三角形;③AC=AO+AP;④S△ABC=S四边形AOCP.其中正确的有( )个.
查看习题详情和答案>>
我们知道:如果两个三角形不仅是相似三角形,而且每对对应点所在的直线都经过同一个点,那么这两个三角形叫做位似三角形,它们的相似比又称为位似比,这个点叫做位似中心.利用三角形的位似可以将一个三角形缩小或放大.
(1)选择:如图1,点O是等边三角形PQR的中心,P′、Q′、R′分别是OP、OQ、OR的中点,则△P′Q′R′与△PQR是位似三角形.此时,△P′Q′R′与△PQR的位似比、位似中心分别为 ;
(A)2、点P,(B)
、点P,( C)2、点O,(D)
、点O;
(2)如图2,用下面的方法可以画△AOB的内接等边三角形.阅读后证明相应问题 .
.
画法:
①在△AOB内画等边三角形CDE,使点C在OA上,点D在OB上;
②连接OE并延长,交AB于点E′,过点E′作E′C′∥EC,交OA于点C′,作E′D′∥ED,交OB于点D′;
③连接C′D′,则△C′D′E′是△AOB的内接三角形.
求证:△C′D′E′是等边三角形. 查看习题详情和答案>>
(1)选择:如图1,点O是等边三角形PQR的中心,P′、Q′、R′分别是OP、OQ、OR的中点,则△P′Q′R′与△PQR是位似三角形.此时,△P′Q′R′与△PQR的位似比、位似中心分别为
(A)2、点P,(B)
| 1 |
| 2 |
| 1 |
| 2 |
(2)如图2,用下面的方法可以画△AOB的内接等边三角形.阅读后证明相应问题
 .
.画法:
①在△AOB内画等边三角形CDE,使点C在OA上,点D在OB上;
②连接OE并延长,交AB于点E′,过点E′作E′C′∥EC,交OA于点C′,作E′D′∥ED,交OB于点D′;
③连接C′D′,则△C′D′E′是△AOB的内接三角形.
求证:△C′D′E′是等边三角形. 查看习题详情和答案>>