摘要：解:(1)在Rt△DBE中.BE=1.DE=.∴BD=== AB.∴ 则D为AB中点, 而AC=BC. ∴CD⊥AB 又∵三棱柱ABC-A1B1C1为直三棱柱, ∴CD⊥AA1 又 AA1∩AB=A 且 AA1.AB Ì 平面A1ABB1 故 CD⊥平面A1ABB1 6分(2)解:∵A1ABB1为矩形.∴△A1AD.△DBE.△EB1A1都是直角三角形.
网址：http://m.1010jiajiao.com/timu_id_473695[举报]
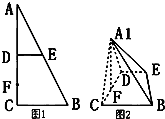如图1，在Rt△ABC中，∠C=90°，D，E分别是AC，AB上的中点，将△ADE沿DE折起到△A1DE的位置，作A1F⊥CD，垂足为F，如图2．
（1）求证：DE∥平面A1CB；
（2）求证：A1F⊥BE；
（3）若∠A=45°，AC=2，在线段CD上是否存在点F，使得二面角A1-BE-F为45°．若存在，则指出点F的位置，若不存在，请说明理由．
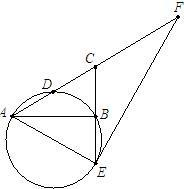已知：如图，在Rt△ABC中，∠ABC=90°，D是AC的中点，CB的延长线交过A、B、D三点的圆于点E．（1）判断线段AE与CE之间的数量关系，并加以证明；
（2）若过A、B、D三点的圆记为⊙O，过E点作⊙O的切线交AC的延长线于点F，且CD：CF=1：2，求：cosF的值． 查看习题详情和答案>>
选修4-1：几何证明选讲．
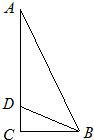如图，在Rt△ABC中，AC⊥BC，D在边AC上，已知BC=2，CD=1，∠ABD=45°，则AD=
（2012•北京）如图1，在Rt△ABC中，∠C=90°，D，E分别为AC，AB的中点，点F为线段CD上的一点，将△ADE沿DE折起到△A1DE的位置，使A1F⊥CD，如图2．