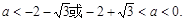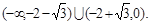摘要:解之得或(舍)
网址:http://m.1010jiajiao.com/timu_id_471460[举报]
已知函数 其中
其中 为自然对数的底数,
为自然对数的底数,
 .(Ⅰ)设
.(Ⅰ)设 ,求函数
,求函数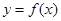 的最值;(Ⅱ)若对于任意的
的最值;(Ⅱ)若对于任意的 ,都有
,都有 成立,求
成立,求 的取值范围.
的取值范围.
【解析】第一问中,当 时,
时, ,
, .结合表格和导数的知识判定单调性和极值,进而得到最值。
.结合表格和导数的知识判定单调性和极值,进而得到最值。
第二问中,∵ ,
, ,
,
∴原不等式等价于: ,
,
即 , 亦即
, 亦即
分离参数的思想求解参数的范围
解:(Ⅰ)当 时,
时, ,
, .
.
当 在
在 上变化时,
上变化时, ,
, 的变化情况如下表:
的变化情况如下表:
|
|
|
|
|
|
|
|
|
|
- |
|
+ |
|
|
|
|
|
|
|
1/e |
∴ 时,
时, ,
, .
.
(Ⅱ)∵ ,
, ,
,
∴原不等式等价于: ,
,
即 , 亦即
, 亦即 .
.
∴对于任意的 ,原不等式恒成立,等价于
,原不等式恒成立,等价于 对
对 恒成立,
恒成立,
∵对于任意的 时,
时, 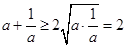 (当且仅当
(当且仅当 时取等号).
时取等号).
∴只需 ,即
,即 ,解之得
,解之得 或
或 .
.
因此, 的取值范围是
的取值范围是
查看习题详情和答案>>
已知点A(7,1),B(1,4),若直线y=ax与线段AB交于点C,且 =2
=2 ,则实数a=________.
,则实数a=________.
[答案] 1
[解析] 设C(x0,ax0),则 =(x0-7,ax0-1),
=(x0-7,ax0-1), =(1-x0,4-ax0),
=(1-x0,4-ax0),
∵ =2
=2 ,∴
,∴ ,解之得
,解之得 .
.
查看习题详情和答案>>
【解析】如图:|OB|=b,|O F1|=c.∴kPQ=![]() ,kMN=﹣
,kMN=﹣![]() .
.
直线PQ为:y=![]() (x+c),两条渐近线为:y=
(x+c),两条渐近线为:y=![]() x.由
x.由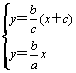 ,得:Q(
,得:Q(![]() ,
,![]() );由
);由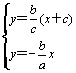 ,得:P(
,得:P(![]() ,
,![]() ).∴直线MN为:y-
).∴直线MN为:y-![]() =﹣
=﹣![]() (x-
(x-![]() ),
),
令y=0得:xM=![]() .又∵|MF2|=|F1F2|=2c,∴3c=xM=
.又∵|MF2|=|F1F2|=2c,∴3c=xM=![]() ,解之得:
,解之得:![]() ,即e=
,即e=![]() .
.
【答案】B
查看习题详情和答案>>
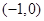






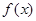 的二次项系数为
的二次项系数为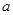 ,且不等式
,且不等式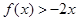 的解集为
的解集为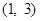 ,
,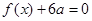 有两个相等的根,求
有两个相等的根,求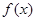 的最大值为正数,求
的最大值为正数,求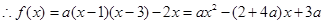 ①
①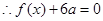
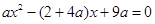 ②
②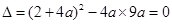 ,
,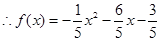
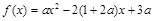
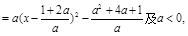
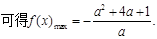
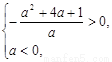 解得:
解得: