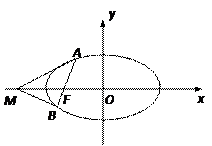
摘要：(2)过F作一条与两坐标都不垂直的直线l交椭圆于P.Q两点.在x轴上是否存在点N.使得NF恰好为PNQ的内角评分线.若存在.求出点N的坐标.若不存在.请说明理由.学科网
网址：http://m.1010jiajiao.com/timu_id_471409[举报]
过椭圆
的左焦点F任作一条与两坐标轴都不垂直的弦AB，若x轴上的定点M，总能使得MF为△AMB的一条内角平分线，则称点M为该椭圆的“左特征点”．
①求椭圆
的“左特征点”M的坐标；0
②试根据①中的结论猜测：椭圆
的“左特征点”M是一个怎样的点？并证明你的结论
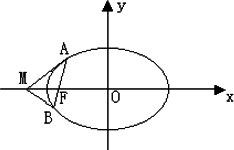
过椭圆
的左焦点F任作一条与两坐标轴都不垂直的弦AB，若点M在x轴上，且使得MF为△AMB的一条内角平分线，则称点M为该椭圆的“左特征点”．
(1)求椭圆
的“左特征点”M的坐标；
(2)试根据(1)中的结论猜测：椭圆
的“左特征点”M是一个怎样的点？并证明你的结论．
过椭圆
=1(a＞b＞0)的左焦点F任作一条与两坐标轴都不垂直的弦AB，若点M在x轴上，且使得MF为△AMB的一条内角平分线，则称点M为该椭圆的“左特征点”，那么“左特征点”M一定是（ ）
=1(a＞b＞0)的左焦点F任作一条与两坐标轴都不垂直的弦AB，若点M在x轴上，且使得MF为△AMB的一条内角平分线，则称点M为该椭圆的“左特征点”，那么“左特征点”M一定是（ ）A.椭圆左准线与x轴的交点 B.坐标原点
C.椭圆右准线与x轴的交点 D.右焦点
查看习题详情和答案>>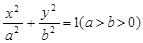
的左焦点F任作一条与两坐标轴都不垂直的弦AB，若点M在x轴上，且使得MF为△AMB的一条内角平分线，则称点M为该椭圆的“左特征点”．求椭圆
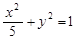的“左特征点”M的坐标；
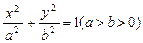的左焦点F任作一条与两坐标轴都不垂直的弦AB，若点M在x轴上，且使得MF为△AMB的一条内角平分线，则称点M为该椭圆的“左特征点”．求椭圆
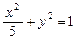的“左特征点”M的坐标；