题目内容
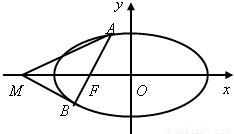
过椭圆![]() 的左焦点F任作一条与两坐标轴都不垂直的弦AB,若点M在x轴上,且使得MF为△AMB的一条内角平分线,则称点M为该椭圆的“左特征点”.
的左焦点F任作一条与两坐标轴都不垂直的弦AB,若点M在x轴上,且使得MF为△AMB的一条内角平分线,则称点M为该椭圆的“左特征点”.
(1)求椭圆![]() 的“左特征点”M的坐标;
的“左特征点”M的坐标;
(2)试根据(1)中的结论猜测:椭圆![]() 的“左特征点”M是一个怎样的点?并证明你的结论.
的“左特征点”M是一个怎样的点?并证明你的结论.
答案:
解析:
解析:
|
解:(1)设 ∵ 即 于是 (2)对于椭圆 证明:设椭圆的左准线 据椭圆第二定义: 于是 ∴ |

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
 已知离心率为
已知离心率为

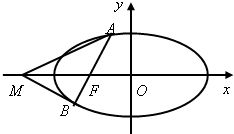
 的左焦点F任作一条与两坐标轴都不垂直的弦AB,若点M在x轴上,且使得MF为△AMB的一条内角平分线,则称点M为该椭圆的“左特征点”.求椭圆
的左焦点F任作一条与两坐标轴都不垂直的弦AB,若点M在x轴上,且使得MF为△AMB的一条内角平分线,则称点M为该椭圆的“左特征点”.求椭圆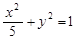 的“左特征点”M的坐标;
的“左特征点”M的坐标;
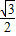 的椭圆
的椭圆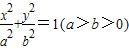 上的点到左焦点F的最长距离为
上的点到左焦点F的最长距离为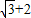 .
.