摘要:[解](1)解:依题意双曲线方程可化为则
网址:http://m.1010jiajiao.com/timu_id_471377[举报]
已知函数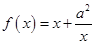 ,
,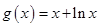 ,其中
,其中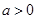 .
.
(1)若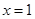 是函数
是函数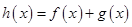 的极值点,求实数
的极值点,求实数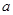 的值;
的值;
(2)若对任意的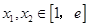 (
(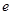 为自然对数的底数)都有
为自然对数的底数)都有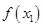 ≥
≥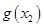 成立,求实数
成立,求实数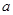 的取值范围.
的取值范围.
【解析】(1)根据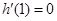 建立关于a的方程求a即可.
建立关于a的方程求a即可.
(2)本题要分别求出f(x)在[1,e]上的最小值,g(x)在[1,e]上的最大值,然后
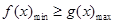 ,解关于a的不等式即可.
,解关于a的不等式即可.
查看习题详情和答案>>
已知椭圆C: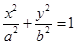
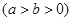 的一个顶点为A(2,0),离心率为
的一个顶点为A(2,0),离心率为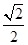 ,直线
,直线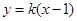 与椭圆C交于不同的两点M,N。
与椭圆C交于不同的两点M,N。
(1) 求椭圆C的方程
(2) 当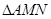 的面积为
的面积为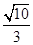 时,求k的值。
时,求k的值。
【解析】(1)∵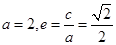 ∴
∴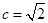 ∴
∴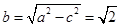 ∴
∴
(2)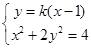
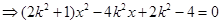
∴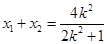 ,
,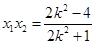
∴
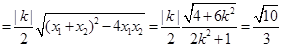
化简得: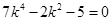 ,解得
,解得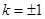
查看习题详情和答案>>
已知曲线C: (m∈R)
(m∈R)
(1) 若曲线C是焦点在x轴点上的椭圆,求m的取值范围;
(2) 设m=4,曲线c与y轴的交点为A,B(点A位于点B的上方),直线y=kx+4与曲线c交于不同的两点M、N,直线y=1与直线BM交于点G.求证:A,G,N三点共线。
【解析】(1)曲线C是焦点在x轴上的椭圆,当且仅当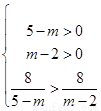 解得
解得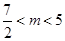 ,所以m的取值范围是
,所以m的取值范围是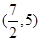
(2)当m=4时,曲线C的方程为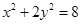 ,点A,B的坐标分别为
,点A,B的坐标分别为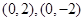 ,
,
由 ,得
,得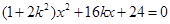
因为直线与曲线C交于不同的两点,所以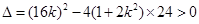
即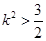
设点M,N的坐标分别为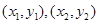 ,则
,则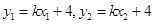
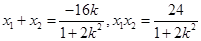
直线BM的方程为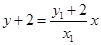 ,点G的坐标为
,点G的坐标为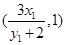
因为直线AN和直线AG的斜率分别为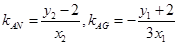
所以
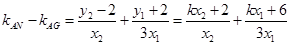
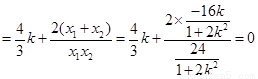
即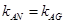 ,故A,G,N三点共线。
,故A,G,N三点共线。
查看习题详情和答案>>
 .
.
 即可.
即可. 就是直线AC与平面AB1D1所成的角.然后解三角形即可.
就是直线AC与平面AB1D1所成的角.然后解三角形即可. 是等差数列,其前n项和为Sn,
是等差数列,其前n项和为Sn, 是等比数列,且
是等比数列,且 ,
, .
. ,
, ,证明
,证明 (
( 的公差为d,等比数列
的公差为d,等比数列 的公比为q.
的公比为q. ,得
,得 ,
, ,
, .
. ,解得
,解得
 ,
, ,
, .
. ①
① ②
②



 ,
,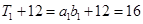 ,
, ,故等式成立.
,故等式成立. ,则当n=k+1时,有:
,则当n=k+1时,有:





 ,因此n=k+1时等式也成立
,因此n=k+1时等式也成立