网址：http://m.1010jiajiao.com/timu_id_46962[举报]
一、选择题1．B 2.B 3. C 4.D 5.D 6. D 7.C 8.B 9.D 10.A
二、填空题11.
， 12. 
， 13.
2个， 14. 小李， 15. 12π
16. 3
17.
18．
三、19.
解：解不等式①，得
x>
………………………2分
解不等式②，得 x≤3…………………………4分
所以原不等式组的解集是
…………………………6分
………………………………7分
20.
（1）AE=
（2）会影响采光，说理充分。………………………………………… 7分
21.解：（1）该游戏规则不公平……………………………………………………1分
每次游戏可能出现的所有结果列表如下：
哥哥的数字
小明的
数字
2
5
6
8
3
（2，3）
（5，3）
（6，3）
（8，3）
4
（2，4）
（5，4）
（6，4）
（8，4）
7
（2，7）
（5，7）
（6，7）
（8，7）
9
（2，9）
（5，9）
（6，9）
（8，9）
根据表格，数字之和的情况共有16种，其中和为偶数的有6种：
（5，3）、（2，4）、（6，4）、（8，4）、（5，7）、（5，9）
∴小明获胜的概率
………………………………………………………5分
∴哥哥获胜的概率为
∴该游戏规则不公平…………………………………………………………………8分
（2）将小明的奇数数字扑克牌与哥哥偶数数字扑克牌对换一张 ……………10分
22.解：（1）根据轴反射的性质可知，在△AFE与△
FB中，
∵∠A＝∠，AE＝B，∠AFE＝∠FB，
∴△AFE≌△FB………………………………………………2分
∴AF＝F ……………………………………………………4分
（2）根据平移的性质可知
为平移的距离. 在Rt△
中，
，
所以
………………………………………6分
（3）根据旋转的性质可知，△
为等边三角形，∠
为旋转角.
∴旋转角∠为30°. ……………………………………8分
23.解：21．（1）
…………………………………………2分
（2）
…………………………………………6分
（3）设收益为
，则
，
时，
，……………8分
即
月上市出售这种蔬菜每千克收益最大，最大受益为
元．……………………10分
24.（1）如图①结论：
．????????????????????????????????????????????????????????????????????? 2分
证明：过
作
于
，则
，
，
．
四边形
为正方形，
，
四边形
为正方形， 
， 
．
四边形
为矩形．
，
．?????????????????????????????????? 3分
在
和
中，
，
．
，
?????????????????????????????????????????????????????????????????????????????????????????????????????? 4分
，
，
．????????????????????????????????? 5分
，
，
．???????????????????????????????????????????????????????????????????????????????????????????????????? 6分
（2）如图②，若点
在
的延长线上时，结论
．???????????????????????????? 8分
（3）如图，若点
在线段
上时，结论：
??????????????????????????????????? 9分
若点
在射线
上时，结论：
．???????????????????????????????????????????????? 10分
 |
25．解：（1）设挂式空调和电风扇每台的采购价格分别为
元和
元
依题意，得
???????????????????????????????????????????????????????????????????????? 5分
解得
即挂式空调和电风扇每台的采购价分别为
元和
元．?????????????????????????????? 6分
（2）设该业主计划购进空调
台，则购进电风扇
台
则
解得：
为整数 
为9，10，11????????????????????????????????????????????????????????????????????????? 7分
故有三种进货方案，分别是：方案一：购进空调9台，电风扇61台；
方案二：购进空调10台，电风扇60台；
方案三：购进空调11台，电风扇59台．??????????????? 8分
设这两种电器销售完后，所获得的利润为
，则
由于随的增大而增大．
故当
时，有最大值，
即选择第3种进货方案获利最大，最大利润为3970 …………………12分
26.解：（1）由题意可知，
，
，
点坐标为
．???????????????????????????????????????????????????????????????????????????????????????? 2分
（2）设
的面积为
，在中，
，
边上的高为
，其中，
． 3分
．????????????????????????????????????????????? 5分
的最大值为
，此时
．???????????????????????????????????????????????????????????????????????????????? 7分
（3）延长
交
于，则有
．
①若
，
．
，
．……………………………………9分
②若
，则
，
．???????????????????????????????????????????????????????????????????????????????????????????????? 10分
③若
，则
．
，
在
中，
．
，
．????????????????????????????????????????????????????????????? 11分
综上所述，
，或
，或
． ………………………………………12分
（1）确定A、C、D三点的坐标；
（2）求过B、C、D三点的抛物线的解析式；
（3）若过点（0，3）且平行于x轴的直线与（2）小题中所求抛物线交于M、N两点，以MN为一边，抛物线上任意一点P（x，y）为顶点作平行四边形，若平行四边形的面积为S，写出S关于P点纵坐标y的函数解析式；
（4）当
| 1 | 2 |
（1）求m的值，并将平移后的抛物线解析式写成y2=a（x-h）2+k的形式；
（2）将平移后的抛物线在x轴下方的部分沿x轴翻折到x轴上方，与平移后的抛物线没有变化的部分构成一个新的图象．请写出这个图象对应的函数y的解析式，并在所给的平面直角坐标系中直接画出简图，同时写出该函数在-3＜x≤-
| 3 | 2 |
（3）设一次函数y3=nx+3（n≠0），问是否存在正整数n使得（2）中函
数的函数值y=y3时，对应的x的值为-1＜x＜0？若存在，求出n的值；若不存在，说明理由．
查看习题详情和答案>>
B的直线与抛物线交于点C（3，| 9 | 4 |
（1）写出点A坐标；
（2）求抛物线解析式；
（3）在抛物线的BC段上，是否存在一点P，使得四边形ABPC的面积最大？若存在，求出这个最大值及此时点P的坐标；若不存在，请说明理由；
（4）若点M在线段AB上以每秒1个单位长度的速度从A向B运动，同时，点N在射线BC上以每秒2个单位长度的速度从B向C运动，当其中一个点停止运动时，另一个点也随之停止运动．设运动时间为t秒，当t为何值，△MNB为等腰三角形，写出计算过程．
＜x＜4时，（3）小题中平行四边形的面积是否有最大值？若有，请求出；若无，请说明理由．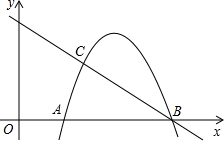
B的直线与抛物线交于点C（3，
）．