题目内容
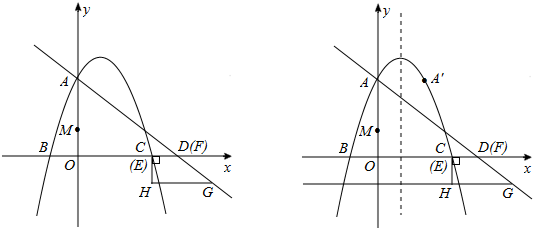
如图,已知抛物线对称轴为直线x=4,且与x轴交于A、B两点(A在B左侧),B点坐标为(6,0),过点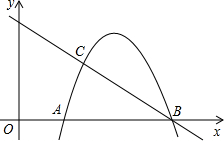 B的直线与抛物线交于点C(3,
B的直线与抛物线交于点C(3,
).
(1)写出点A坐标;
(2)求抛物线解析式;
(3)在抛物线的BC段上,是否存在一点P,使得四边形ABPC的面积最大?若存在,求出这个最大值及此时点P的坐标;若不存在,请说明理由;
(4)若点M在线段AB上以每秒1个单位长度的速度从A向B运动,同时,点N在射线BC上以每秒2个单位长度的速度从B向C运动,当其中一个点停止运动时,另一个点也随之停止运动.设运动时间为t秒,当t为何值,△MNB为等腰三角形,写出计算过程.
 B的直线与抛物线交于点C(3,
B的直线与抛物线交于点C(3,| 9 | 4 |
(1)写出点A坐标;
(2)求抛物线解析式;
(3)在抛物线的BC段上,是否存在一点P,使得四边形ABPC的面积最大?若存在,求出这个最大值及此时点P的坐标;若不存在,请说明理由;
(4)若点M在线段AB上以每秒1个单位长度的速度从A向B运动,同时,点N在射线BC上以每秒2个单位长度的速度从B向C运动,当其中一个点停止运动时,另一个点也随之停止运动.设运动时间为t秒,当t为何值,△MNB为等腰三角形,写出计算过程.
分析:(1)根据二次函数的对称性,利用点B的坐标与对称轴求解;
(2)利用待定系数法求二次函数解析式列式计算即可得解;
(3)假设存在,根据抛物线解析式设点P的坐标为(x,-
x2+6x-9),过点C作CE⊥AB于点E,过点P作PF⊥x轴于点F,则S四边形ABPC=S△ACE+S梯形CEFP+S△BPF,再根据三角形的面积公式与梯形的面积公式列式整理,然后根据二次函数的最值问题解答;
(4)根据A、B的坐标求出AB的长度,根据勾股定理求出BC的值,再分①BN=MN时,过点N作ND⊥BM于点D,然后利用∠ABC的余弦列式计算即可得解,②BN=BM时,用t表示出BM、BN,列出方程计算即可得解,③BM=MN时,过点M作MH⊥BN于点H,然后利用∠ABC的余弦列式计算即可得解.
(2)利用待定系数法求二次函数解析式列式计算即可得解;
(3)假设存在,根据抛物线解析式设点P的坐标为(x,-
| 3 |
| 4 |
(4)根据A、B的坐标求出AB的长度,根据勾股定理求出BC的值,再分①BN=MN时,过点N作ND⊥BM于点D,然后利用∠ABC的余弦列式计算即可得解,②BN=BM时,用t表示出BM、BN,列出方程计算即可得解,③BM=MN时,过点M作MH⊥BN于点H,然后利用∠ABC的余弦列式计算即可得解.
解答:解:(1)∵B点坐标为(6,0),抛物线对称轴为直线x=4,
4×2-6=2,
∴点A的坐标为(2,0);
(2)设抛物线解析式为y=ax2+bx+c,
∵A(2,0),B(6,0),C(3,
),
∴
,
解得
,
∴抛物线解析式为y=-
x2+6x-9;
 (3)存在.理由如下:
(3)存在.理由如下:
如图,设存在点P(x,-
x2+6x-9),使得四边形ABPC的面积最大,
过点C作CE⊥AB于点E,过点P作PF⊥x轴于点F,
∵A(2,0),B(6,0),C(3,
),
∴S四边形ABPC=S△ACE+S梯形CEFP+S△BPF
=
×(3-2)×
+
(
-
x2+6x-9)×(x-3)+
×(6-x)×(-
x2+6x-9)
=
+
(x-3)+
(-
x2+6x-9)×(x-3)+
×(6-x)×(-
x2+6x-9)
=-
(x2-9x+14)
=-
(x-
)2+
,
∵3<
<6,
∴当x=
时,四边形ABPC的面积有最大值,最大值为
,
此时,-
x2+6x-9=-
×(
)2+6×
-9=
,
∴点P的坐标为(
,
);
 (4)∵A(2,0),B(6,0),
(4)∵A(2,0),B(6,0),
∴AB=6-2=4,
∵B(6,0),C(3,
),
∴BC=
=
.
①BN=MN时,如图,过点N作ND⊥BM于点D,则BD=MD=
(4-t),
cos∠ABC=
=
,
解得t=
,
②BN=BM时,如图,BM=4-t,BN=2t,
所以,4-t=2t,
解得t=
,
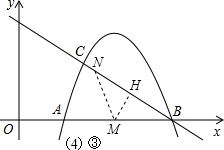 ③BM=MN时,如图,过点M作MH⊥BN于点H,
③BM=MN时,如图,过点M作MH⊥BN于点H,
则BH=
BN=
×2t=t,
BM=4-t,
cos∠ABC=
=
,
解得t=
,
综上所述,当t为
或
或
秒时,△MNB为等腰三角形.
4×2-6=2,
∴点A的坐标为(2,0);
(2)设抛物线解析式为y=ax2+bx+c,
∵A(2,0),B(6,0),C(3,
| 9 |
| 4 |
∴
|
解得
|
∴抛物线解析式为y=-
| 3 |
| 4 |
 (3)存在.理由如下:
(3)存在.理由如下:如图,设存在点P(x,-
| 3 |
| 4 |
过点C作CE⊥AB于点E,过点P作PF⊥x轴于点F,
∵A(2,0),B(6,0),C(3,
| 9 |
| 4 |
∴S四边形ABPC=S△ACE+S梯形CEFP+S△BPF
=
| 1 |
| 2 |
| 9 |
| 4 |
| 1 |
| 2 |
| 9 |
| 4 |
| 3 |
| 4 |
| 1 |
| 2 |
| 3 |
| 4 |
=
| 9 |
| 8 |
| 9 |
| 8 |
| 1 |
| 2 |
| 3 |
| 4 |
| 1 |
| 2 |
| 3 |
| 4 |
=-
| 9 |
| 8 |
=-
| 9 |
| 8 |
| 9 |
| 2 |
| 225 |
| 32 |
∵3<
| 9 |
| 2 |
∴当x=
| 9 |
| 2 |
| 225 |
| 32 |
此时,-
| 3 |
| 4 |
| 3 |
| 4 |
| 9 |
| 2 |
| 9 |
| 2 |
| 45 |
| 16 |
∴点P的坐标为(
| 9 |
| 2 |
| 45 |
| 16 |
 (4)∵A(2,0),B(6,0),
(4)∵A(2,0),B(6,0),∴AB=6-2=4,
∵B(6,0),C(3,
| 9 |
| 4 |
∴BC=
(6-3)2+(
|
| 15 |
| 4 |
①BN=MN时,如图,过点N作ND⊥BM于点D,则BD=MD=
| 1 |
| 2 |
cos∠ABC=
| ||
| 2t |
| 6-3 | ||
|
解得t=
| 20 |
| 21 |
②BN=BM时,如图,BM=4-t,BN=2t,
所以,4-t=2t,
解得t=
| 4 |
| 3 |
 ③BM=MN时,如图,过点M作MH⊥BN于点H,
③BM=MN时,如图,过点M作MH⊥BN于点H,则BH=
| 1 |
| 2 |
| 1 |
| 2 |
BM=4-t,
cos∠ABC=
| t |
| 4-t |
| 6-3 | ||
|
解得t=
| 16 |
| 9 |
综上所述,当t为
| 20 |
| 21 |
| 4 |
| 3 |
| 16 |
| 9 |
点评:本题综合考查了二次函数,主要利用了二次函数的对称性,待定系数法求二次函数解析式,不规则图形的面积的求解,二次函数的最值问题,以及等腰三角形的性质,(3)运算量比较大,计算时要认真仔细,(4)要根据等腰三角形腰的不同分情况讨论.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
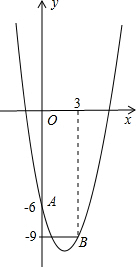 如图,已知抛物线y=ax2-4x+c经过点A(0,-6)和B(3,-9).
如图,已知抛物线y=ax2-4x+c经过点A(0,-6)和B(3,-9). 的左侧),点B的横坐标是1;
的左侧),点B的横坐标是1;