摘要：综上所述:只有时满足条件.故.----14′
网址：http://m.1010jiajiao.com/timu_id_467730[举报]
已知函数f（x）=ax2+bx（a，b为常数，且a≠0）满足条件f（1-x）=f（1+x），且函数g（x）=f（x）-x只有一个零点．
（Ⅰ）求函数f（x）的解析式；
（Ⅱ）求实数m，n（m＜n），使得f（x）的定义域为[m，n]时，f（x）的取值范围是[3m，3n]． 查看习题详情和答案>>
（Ⅰ）求函数f（x）的解析式；
（Ⅱ）求实数m，n（m＜n），使得f（x）的定义域为[m，n]时，f（x）的取值范围是[3m，3n]． 查看习题详情和答案>>
（本小题满分12分）
设二次函数f(x)=ax2+bx(a≠0)满足条件：
①f(-1+x)=f(-1-x)；②函数f(x)的图象与直线y=x只有一个公共点.
(Ⅰ)求f(x)的解析式；
（Ⅱ）若不等式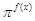
＞（
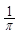）2-tx在t∈［-2，2］时恒成立，求实数x的取值范围.
查看习题详情和答案>>
已知函数f（x）=ax2+bx（a，b为常数，且a≠0）满足条件f（1-x）=f（1+x），且函数g（x）=f（x）-x只有一个零点．
（Ⅰ）求函数f（x）的解析式；
（Ⅱ）求实数m，n（m＜n），使得f（x）的定义域为[m，n]时，f（x）的取值范围是[3m，3n]．
查看习题详情和答案>>
（Ⅰ）求函数f（x）的解析式；
（Ⅱ）求实数m，n（m＜n），使得f（x）的定义域为[m，n]时，f（x）的取值范围是[3m，3n]．
查看习题详情和答案>>