摘要:曲线的方程可写成:.∴
网址:http://m.1010jiajiao.com/timu_id_467700[举报]
设x,y满足如下条件:以1 , |x| ,
为三边可构成锐角三角形,在直角坐标平面上可以作出所有这样的以(x,y)为坐标的点集,则限定这个点集的曲线方程为(写出最简形式):
查看习题详情和答案>>
| -y |
y=-x2-1,y=-x2+1,y=x2-1
y=-x2-1,y=-x2+1,y=x2-1
.拓展探究题
(1)已知两个圆:①x2+y2=1;②x2+(y-3)2=1,则由①式减去②式可得两圆的对称轴方程.将上述命题在曲线仍为圆的情况下加以推广,即要求得到一个更一般的命题,而已知命题应成为所推广命题的一个特例.推广的命题为
(2)平面几何中有正确命题:“正三角形内任意一点到三边的距离之和等于定值,大小为边长的
倍”,请你写出此命题在立体几何中类似的真命题:
查看习题详情和答案>>
(1)已知两个圆:①x2+y2=1;②x2+(y-3)2=1,则由①式减去②式可得两圆的对称轴方程.将上述命题在曲线仍为圆的情况下加以推广,即要求得到一个更一般的命题,而已知命题应成为所推广命题的一个特例.推广的命题为
已知两个圆:①(x-a)2+(y-b)2=r2;②(x-c)2+(y-d)2=r2,则由①式减去②式可得两圆的对称轴方程
已知两个圆:①(x-a)2+(y-b)2=r2;②(x-c)2+(y-d)2=r2,则由①式减去②式可得两圆的对称轴方程
.(2)平面几何中有正确命题:“正三角形内任意一点到三边的距离之和等于定值,大小为边长的
| ||
| 2 |
正四面体内任意一点到四个面的距离之和是一个定值,大小为棱长的
倍
| ||
| 3 |
正四面体内任意一点到四个面的距离之和是一个定值,大小为棱长的
倍
.
| ||
| 3 |
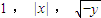 为三边可构成锐角三角形,在直角坐标平面上可以作出所有这样的以(x,y)为坐标的点集,则限定这个点集的曲线方程为(写出最简形式): .
为三边可构成锐角三角形,在直角坐标平面上可以作出所有这样的以(x,y)为坐标的点集,则限定这个点集的曲线方程为(写出最简形式): .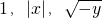 为三边可构成锐角三角形,在直角坐标平面上可以作出所有这样的以(x,y)为坐标的点集,则限定这个点集的曲线方程为(写出最简形式):________.
为三边可构成锐角三角形,在直角坐标平面上可以作出所有这样的以(x,y)为坐标的点集,则限定这个点集的曲线方程为(写出最简形式):________.