题目内容
设x,y满足如下条件:以1 , |x| ,
为三边可构成锐角三角形,在直角坐标平面上可以作出所有这样的以(x,y)为坐标的点集,则限定这个点集的曲线方程为(写出最简形式):
| -y |
y=-x2-1,y=-x2+1,y=x2-1
y=-x2-1,y=-x2+1,y=x2-1
.分析:根据以1 , |x| ,
为三边可构成锐角三角形,利用余弦定理可得:1+x2+y>0且1-y-x2>0,x2-y-1>0同时成立,从而可解.
| -y |
解答:解:由题意,∵以1 , |x| ,
为三边可构成锐角三角形
∴利用余弦定理得:1+x2+y>0且1-y-x2>0,x2-y-1>0同时成立
所以限定这个点集的曲线方程为y=-x2-1,y=-x2+1,y=x2-1
故答案为y=-x2-1,y=-x2+1,y=x2-1
| -y |
∴利用余弦定理得:1+x2+y>0且1-y-x2>0,x2-y-1>0同时成立
所以限定这个点集的曲线方程为y=-x2-1,y=-x2+1,y=x2-1
故答案为y=-x2-1,y=-x2+1,y=x2-1
点评:本题以构成锐角三角形为前提,考查余弦定理的运用,考查轨迹方程,关键是理解构成锐角三角形的条件.

练习册系列答案
相关题目
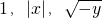 为三边可构成锐角三角形,在直角坐标平面上可以作出所有这样的以(x,y)为坐标的点集,则限定这个点集的曲线方程为(写出最简形式):________.
为三边可构成锐角三角形,在直角坐标平面上可以作出所有这样的以(x,y)为坐标的点集,则限定这个点集的曲线方程为(写出最简形式):________.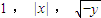 为三边可构成锐角三角形,在直角坐标平面上可以作出所有这样的以(x,y)为坐标的点集,则限定这个点集的曲线方程为(写出最简形式): .
为三边可构成锐角三角形,在直角坐标平面上可以作出所有这样的以(x,y)为坐标的点集,则限定这个点集的曲线方程为(写出最简形式): .