摘要:故满足条件的直线l有两条.其方程分别为y=和
网址:http://m.1010jiajiao.com/timu_id_467173[举报]
下列是有关直线与圆锥曲线的命题:
①过点(2,4)作直线与抛物线y2=8x有且只有一个公共点,这样的直线有2条;
②过抛物线y2=4x的焦点作一条直线与抛物线相交于A,B两点,它们的横坐标之和等于5,则这样的直线有且仅有两条;
③过点(3,1)作直线与双曲线
-y2=1有且只有一个公共点,这样的直线有3条;
④过双曲线x2-
=1的右焦点作直线l交双曲线于A,B两点,若|AB|=4,则满足条件的直线l有3条;
⑤已知双曲线x2-
=1和点A(1,1),过点A能作一条直线l,使它与双曲线交于P,Q两点,且点A恰为线段PQ的中点.
其中说法正确的序号有
查看习题详情和答案>>
①过点(2,4)作直线与抛物线y2=8x有且只有一个公共点,这样的直线有2条;
②过抛物线y2=4x的焦点作一条直线与抛物线相交于A,B两点,它们的横坐标之和等于5,则这样的直线有且仅有两条;
③过点(3,1)作直线与双曲线
| x2 |
| 4 |
④过双曲线x2-
| y2 |
| 2 |
⑤已知双曲线x2-
| y2 |
| 2 |
其中说法正确的序号有
①②④
①②④
.(请写出所有正确的序号) 如图,已知椭圆C:
如图,已知椭圆C:| x2 |
| a2 |
| y2 |
| b2 |
| 2 |
| 3 |
(1)求椭圆C的方程;
(2)直线l:y=kx与抛物线E的交点为O,Q,与椭圆c的交点为M,N(N在线段OQ上),且|MO|=|NQ|. 问满足条件的直线l有几条,说明理由.
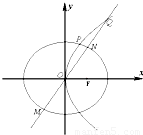
如图,已知椭圆C: 与抛物线E:y2=4x有一个公共的焦点F,且两曲线在第一象限的交点P的横坐标为
与抛物线E:y2=4x有一个公共的焦点F,且两曲线在第一象限的交点P的横坐标为 .
.
(1)求椭圆C的方程;
(2)直线l:y=kx与抛物线E的交点为O,Q,与椭圆c的交点为M,N(N在线段OQ上),且|MO|=|NQ|. 问满足条件的直线l有几条,说明理由.
 查看习题详情和答案>>
查看习题详情和答案>>
 与抛物线E:y2=4x有一个公共的焦点F,且两曲线在第一象限的交点P的横坐标为
与抛物线E:y2=4x有一个公共的焦点F,且两曲线在第一象限的交点P的横坐标为 .
.(1)求椭圆C的方程;
(2)直线l:y=kx与抛物线E的交点为O,Q,与椭圆c的交点为M,N(N在线段OQ上),且|MO|=|NQ|. 问满足条件的直线l有几条,说明理由.
 查看习题详情和答案>>
查看习题详情和答案>>
 如图,已知椭圆C:
如图,已知椭圆C: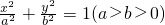 与抛物线E:y2=4x有一个公共的焦点F,且两曲线在第一象限的交点P的横坐标为
与抛物线E:y2=4x有一个公共的焦点F,且两曲线在第一象限的交点P的横坐标为 .
.
(1)求椭圆C的方程;
(2)直线l:y=kx与抛物线E的交点为O,Q,与椭圆c的交点为M,N(N在线段OQ上),且|MO|=|NQ|. 问满足条件的直线l有几条,说明理由.
查看习题详情和答案>>
下列是有关直线与圆锥曲线的命题:
①过点(2,4)作直线与抛物线y2=8x有且只有一个公共点,这样的直线有2条;
②过抛物线y2=4x的焦点作一条直线与抛物线相交于A,B两点,它们的横坐标之和等于5,则这样的直线有且仅有两条;
③过点(3,1)作直线与双曲线
-y2=1有且只有一个公共点,这样的直线有3条;
④过双曲线x2-
=1的右焦点作直线l交双曲线于A,B两点,若|AB|=4,则满足条件的直线l有3条;
⑤已知双曲线x2-
=1和点A(1,1),过点A能作一条直线l,使它与双曲线交于P,Q两点,且点A恰为线段PQ的中点.
其中说法正确的序号有______.(请写出所有正确的序号)
查看习题详情和答案>>
①过点(2,4)作直线与抛物线y2=8x有且只有一个公共点,这样的直线有2条;
②过抛物线y2=4x的焦点作一条直线与抛物线相交于A,B两点,它们的横坐标之和等于5,则这样的直线有且仅有两条;
③过点(3,1)作直线与双曲线
| x2 |
| 4 |
④过双曲线x2-
| y2 |
| 2 |
⑤已知双曲线x2-
| y2 |
| 2 |
其中说法正确的序号有______.(请写出所有正确的序号)