网址:http://m.1010jiajiao.com/timu_id_45015[举报]
一.选择题 1-5 6-10 11-12 BBDBC CBACC DA
二.填空题 13. 1 ; 14. 2; 15. .files/image189.gif) ; 16. -1
; 16. -1
三、解答题
17.解:(Ⅰ)由f(0)=.files/image191.gif) ,得
,得.files/image191.gif) =
=.files/image191.gif) ,∴
,∴.files/image193.gif) ,则a=
,则a=.files/image191.gif) .
.
由f(.files/image145.gif) )=
)=.files/image147.gif) ,得
,得.files/image191.gif) +
+.files/image197.gif) -
-.files/image191.gif) =
=.files/image147.gif) ,∴b=1,…………2分
,∴b=1,…………2分
∴f(x) =.files/image193.gif) cos2x+sinxcosx -
cos2x+sinxcosx -.files/image191.gif) =
=.files/image191.gif) cos2x+
cos2x+.files/image147.gif) sin2x=sin(2x+
sin2x=sin(2x+.files/image199.gif) ).…………4分
).…………4分
(Ⅱ)由f(x)=sin(2x+.files/image199.gif) ).
).
又由.files/image201.gif) +2kπ≤2x+
+2kπ≤2x+.files/image199.gif) ≤
≤.files/image203.gif) +2kπ,得
+2kπ,得.files/image205.gif) +kπ≤x≤
+kπ≤x≤.files/image207.gif) +kπ,
+kπ,
∴f(x)的单调递增区间是[.files/image205.gif) +kπ,
+kπ,.files/image207.gif) +kπ](k∈Z).?…………8分
+kπ](k∈Z).?…………8分
(Ⅲ)∵f(x)=sin2(x+.files/image211.gif) ),
),
∴函数f(x)的图象右移.files/image211.gif) 后对应的函数可成为奇函数.…………12分
后对应的函数可成为奇函数.…………12分
18.解:(I)一次射击后,三人射中目标分别记为事件A1,A2,A3,
由题意知A1,A2,A3互相独立,且.files/image213.gif) ,…………2分
,…………2分
.files/image215.gif) .…………4分
.…………4分
∴一次射击后,三人都射中目标的概率是.files/image217.gif) .…………5分
.…………5分
(Ⅱ)证明:一次射击后,射中目标的次数可能取值为0、1、2、3,相应的没有射中目标的的次数可能取值为3、2、1、0,所以.files/image155.gif) 可能取值为1、3, …………6分
可能取值为1、3, …………6分
则.files/image220.gif)
.files/image222.gif)
.files/image224.gif) )+
)+.files/image226.gif)
.files/image228.gif) ………8分
………8分
∴.files/image230.gif) ,………10分
,………10分
.files/image231.gif) ∴
∴.files/image233.gif) =
=.files/image235.gif) .………12分
.………12分
19.解:(Ⅰ)连接A
∵AC⊥CB,∴BC⊥平面A
∴.files/image237.gif) 为
为.files/image239.gif) 与平面A
与平面A
.files/image241.gif) .
.
∴.files/image243.gif) 与平面A
与平面A.files/image245.gif) .…………3分
.…………3分
(Ⅱ)分别延长AC,A1D交于G. 过C作CM⊥A
∵BC⊥平面ACC
∴BM⊥A
平面A
∴CG=2,DC=1 在直角三角形CDG中,.files/image247.gif) ,
,.files/image249.gif) .……7分
.……7分
即二面角B―A1D―A的大小为.files/image251.gif) .……………………8分
.……………………8分
(Ⅲ)取线段AC的中点F,则EF⊥平面A1BD.……………9分
证明如下:
∵A1B
∵由(Ⅰ)BC⊥平面A
∵EF在平面A
C
同理可证EF⊥BD,∴EF⊥平面A1BD.……………………12分
.files/image253.gif) 解法二:
解法二:
(Ⅰ)同解法一……………………3分
(Ⅱ)∵A1B
AC⊥CB,D、E分别为C
建立如图所示的坐标系得:
C(0,0,0),B(2,0,0),A(0,2,0),
C1(0,0,2), B1(2,0,2), A1(0,2,2),
D(0,0,1), E(1,0,2).………………6分
.files/image255.gif) ,设平面A1BD的法向量为
,设平面A1BD的法向量为.files/image257.gif)
.files/image259.gif) ,
,
.files/image261.gif)
.files/image263.gif) .…………6分
.…………6分
平面ACC.files/image265.gif) =(1,0,0),
=(1,0,0),.files/image267.gif) .………7分
.………7分
即二面角B―A1D―A的大小为.files/image269.gif) .…………………8分
.…………………8分
(Ⅲ)F为AC上的点,故可设其坐标为(0,.files/image271.gif) ,0),∴
,0),∴.files/image273.gif) .
.
由(Ⅱ)知.files/image275.gif) 是平面A1BD的一个法向量,
是平面A1BD的一个法向量,
欲使EF⊥平面A1BD,当且仅当.files/image277.gif) //
//.files/image257.gif) .……10分
.……10分
∴.files/image280.gif) ,∴当F为AC的中点时,EF⊥平面A1BD.…………………12分
,∴当F为AC的中点时,EF⊥平面A1BD.…………………12分
20.解:(Ⅰ) 据题意:.files/image282.gif)
.files/image168.gif) ,
,
.files/image285.gif)
.files/image287.gif) .
.
两式相减,有:.files/image289.gif) ,…………3分
,…………3分
.files/image291.gif)
.files/image287.gif) .…………4分
.…………4分
又由.files/image293.gif) =
=.files/image295.gif) 解得
解得.files/image297.gif) . …………5分
. …………5分
∴.files/image061.gif) 是以
是以.files/image149.gif) 为首项,
为首项,.files/image149.gif) 为公比的等比数列,∴
为公比的等比数列,∴.files/image300.gif) .…………6分
.…………6分
(Ⅱ) .files/image301.gif)
.files/image303.gif) ………8分
………8分
.files/image305.gif)
.files/image307.gif)
.files/image309.gif)
.files/image311.gif) …………12分
…………12分
21.解: (Ⅰ)依题意,由余弦定理得:
.files/image313.gif) , ……2分
, ……2分
即.files/image315.gif)
.files/image317.gif)
.files/image319.gif) .
.
.files/image321.gif) ,即
,即.files/image323.gif) . …………4分
. …………4分
(当动点.files/image102.gif) 与两定点
与两定点.files/image326.gif) 共线时也符合上述结论)
共线时也符合上述结论)
.files/image328.gif) 动点
动点.files/image102.gif) 的轨迹Q是以
的轨迹Q是以.files/image326.gif) 为焦点,实轴长为
为焦点,实轴长为.files/image331.gif) 的双曲线.其方程为
的双曲线.其方程为.files/image333.gif) .………6分
.………6分
(Ⅱ)假设存在定点.files/image335.gif) ,使
,使.files/image337.gif) 为常数.
为常数.
(1)当直线.files/image176.gif) 不与
不与.files/image178.gif) 轴垂直时,
轴垂直时,
设直线.files/image176.gif) 的方程为
的方程为.files/image342.gif) ,代入
,代入.files/image333.gif) 整理得:
整理得:
.files/image344.gif) .…………7分
.…………7分
由题意知,.files/image346.gif) .
.
设.files/image348.gif) ,
,.files/image350.gif) ,则
,则.files/image352.gif) ,
,.files/image354.gif) .…………8分
.…………8分
于是,.files/image356.gif) …………9分
…………9分
.files/image358.gif)
.files/image360.gif) .…………10分
.…………10分
要使.files/image337.gif) 是与
是与.files/image052.gif) 无关的常数,当且仅当
无关的常数,当且仅当.files/image363.gif) ,此时
,此时.files/image365.gif) .…11分
.…11分
(2)当直线.files/image176.gif) 与
与.files/image178.gif) 轴垂直时,可得点
轴垂直时,可得点.files/image367.gif) ,
,.files/image369.gif) ,
,
当.files/image363.gif) 时,
时,.files/image371.gif) .
.
故在.files/image178.gif) 轴上存在定点
轴上存在定点.files/image373.gif) ,使
,使.files/image337.gif) 为常数.…………12分
为常数.…………12分
22.解:(Ⅰ).files/image375.gif) ………1分
………1分
.files/image377.gif)
同理,令.files/image379.gif)
∴f(x)单调递增区间为.files/image381.gif) ,单调递减区间为
,单调递减区间为.files/image383.gif) .……………………3分
.……………………3分
由此可知.files/image385.gif) …………………………………………4分
…………………………………………4分
(Ⅱ)由(I)可知当.files/image387.gif) 时,有
时,有.files/image389.gif) ,
,
即.files/image391.gif) .
.
.files/image393.gif) .……………………………………………………………………7分
.……………………………………………………………………7分
(Ⅲ)
设函数.files/image395.gif) …………………………………10分
…………………………………10分
.files/image397.gif)
∴函数.files/image399.gif) )上单调递增,在
)上单调递增,在.files/image401.gif) 上单调递减.
上单调递减.
∴.files/image403.gif) 的最小值为
的最小值为.files/image405.gif) ,即总有
,即总有.files/image407.gif)
而.files/image409.gif)
.files/image411.gif)
即.files/image413.gif)
令.files/image415.gif) 则
则.files/image417.gif)
.files/image419.gif)
.files/image421.gif) ……………………………………14分
……………………………………14分
(本小题满分12分)
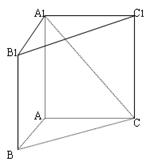
如图,直三棱柱A1B1C1—ABC中,C1C=CB=CA=2,AC⊥CB.
D、E分别为棱C1C、B1C1的中点.
(1)求二面角B—A1D—A的平面角余弦值;
(2)在线段AC上是否存在一点F,使得EF⊥平面A1BD?
若存在,确定其位置并证明结论;若不存在,说明理由.
查看习题详情和答案>>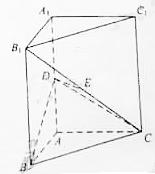
 (Ⅱ)设异面直线AB
(Ⅱ)设异面直线AB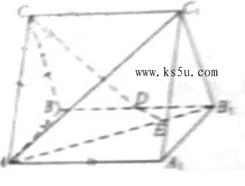 (Ⅱ)设异面直线AB
(Ⅱ)设异面直线AB